作為一名程序員,掌握各種算法可以幫助我們解決各種復雜的問題,提高代碼的效率和性能,同時也是面試中常被考察的重要內容之一。無論是開發新的軟件應用、優化現有的算法邏輯還是解決各類計算問題,算法都是不可或缺的工具。因此,程序員掌握一系列常用的算法,以確保能夠高效地編寫出穩定、功能強大的軟件。
常用的算法類別及其應用如下:
一. 排序算法
1.冒泡排序:用于將一組數據按照升序或降序進行排列,它通過比較相鄰元素的大小來進行交換,直到整個序列排序完成。
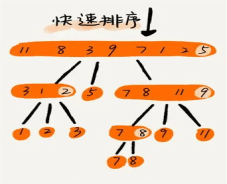
2.快速排序:快速排序是一種常用且高效的排序算法,它采用遞歸的方式將問題劃分為更小的子問題,并使用一個基準元素進行排序。
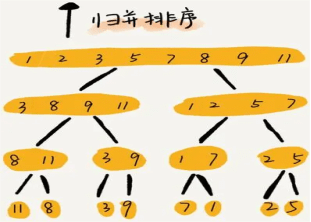
3.歸并排序:歸并排序采用分治策略,將問題逐步細化并通過合并操作得到最終的有序結果。

二. 搜索算法
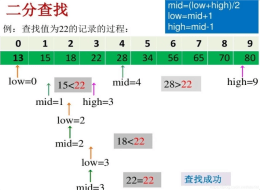
1.二分查找:二分查找適用于有序數組,它將目標值與數組的中間元素進行比較,從而縮小搜索范圍,直到找到目標元素或確定不存在。
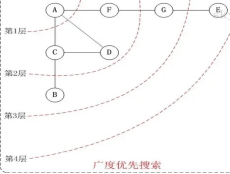
2.廣度優先搜索:廣度優先搜索用于遍歷或搜索圖或樹的結構。它按照層次的順序遍歷節點,先訪問根節點,然后是所有與根節點相鄰的節點,然后是他們的鄰節點,依次類推。
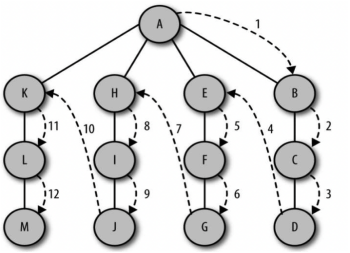
3.深度優先搜索:深度優先搜索也用于遍歷或搜索圖或樹的結構。它從根節點開始,沿著一條路徑搜索到最深的節點,然后再回溯到之前的節點繼續搜索。
三. 圖算法
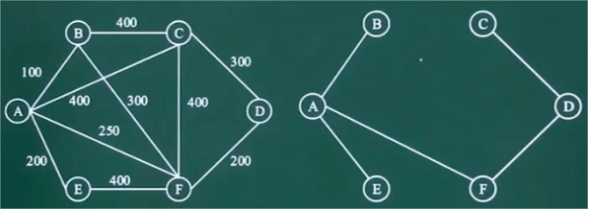
1.最短路徑算法:最短路徑算法用于尋找兩個節點之間的最短路徑。常用的最短路徑算法有Dijkstra算法和Floyd-Warshall算法。
2.最小生成樹算法:最小生成樹算法用于在一個帶權重的無向圖中找出一棵包含所有節點的子樹,并且使得該子樹的邊權重之和最小。常見的最小生成樹算法有Prim算法和Kruskal算法。
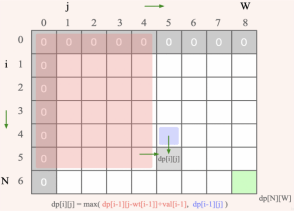
四.動態規劃
1.背包問題:背包問題是一類經典的優化問題,其中給定一組物品和一個背包容量,目標是將物品放入背包中,使得物品總價值最大化,同時不超過背包的容量。
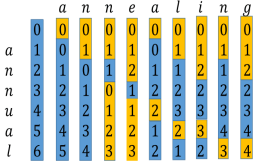
2.最長公共子序列:最長公共子序列問題是一類經典的字符串處理問題,目標是找出兩個字符串中最長的共同子序列的長度。