有高中學(xué)生經(jīng)常問(wèn)我們物理老師:為什么行星繞太陽(yáng)運(yùn)動(dòng)的軌道是橢圓?是圓不更香嗎?嘿嘿,這個(gè)問(wèn)題不說(shuō)高中學(xué)生,我們作為老師都整不明白。作為一種學(xué)習(xí),我在這篇文章里來(lái)詳解這個(gè)為什么。
開(kāi)普勒三大定律是德國(guó)天文學(xué)家開(kāi)普勒提出的關(guān)于行星運(yùn)動(dòng)的三大定律。第一和第二定律發(fā)表于1609年,是開(kāi)普勒從天文學(xué)家第谷觀測(cè)火星位置所得資料中總結(jié)出來(lái)的;第三定律發(fā)表于1619年。這三大定律又分別稱為橢圓定律、面積定律和調(diào)和定律。
開(kāi)普勒定律
①橢圓定律:所有行星繞太陽(yáng)的軌道都是橢圓,太陽(yáng)在橢圓的一個(gè)焦點(diǎn)上。
②面積定律:行星和太陽(yáng)的連線在相等的時(shí)間間隔內(nèi)掃過(guò)的面積相等。
③調(diào)和定律:所有行星繞太陽(yáng)一周的時(shí)間(即周期)的平方與它們軌道半長(zhǎng)軸的立方成正比。
此后,學(xué)者們把第一定律修改成為:所有行星(和彗星)的軌道都屬于圓錐曲線,而太陽(yáng)則在它們的一個(gè)焦點(diǎn)上。第二定律只在行星質(zhì)量比太陽(yáng)質(zhì)量小得多的情況下才是精確的。如果考慮到行星也吸引太陽(yáng),這便是一個(gè)二體問(wèn)題。第三定律也有修正。
太陽(yáng)系示意圖(俯視)
首先我們復(fù)習(xí)一下矢量的微分和求導(dǎo)。如下圖。
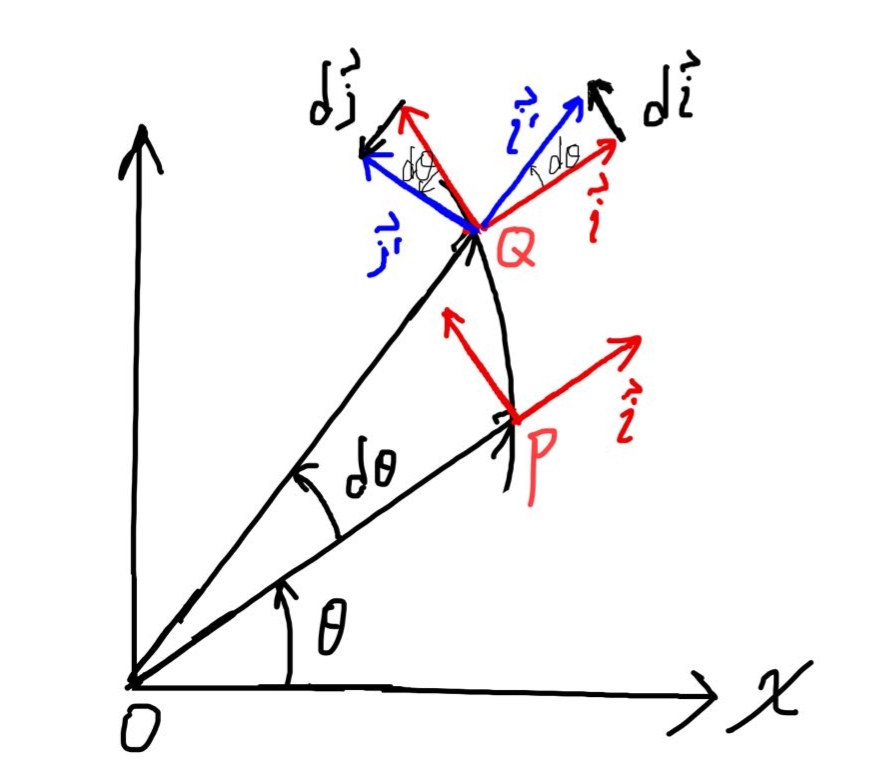
質(zhì)點(diǎn)在極短時(shí)間dt內(nèi)從P點(diǎn)運(yùn)動(dòng)到Q點(diǎn),其極角也從θ轉(zhuǎn)到θ+dθ,徑向單位矢量ⅰ和橫向單位矢量J也都轉(zhuǎn)過(guò)θ
從這張圖里我們可以推導(dǎo)出質(zhì)點(diǎn)的加速度分解成的橫向加速度(垂直于極徑)和徑向加速度。為此我們先看看上圖中橫向單位矢量和徑向單位矢量對(duì)時(shí)間求導(dǎo)會(huì)得出什么。
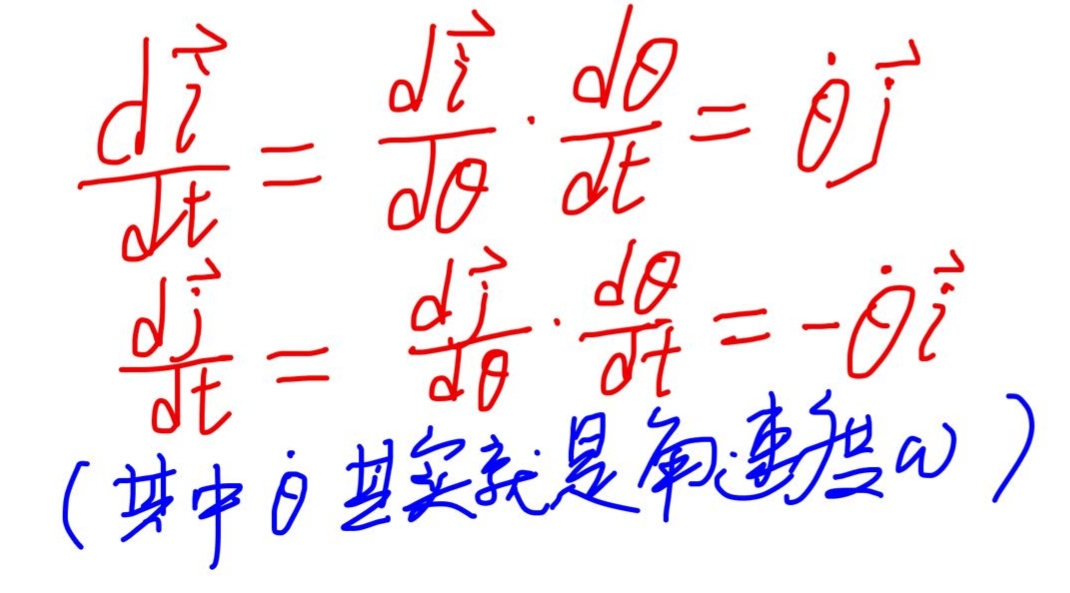
可見(jiàn),這其實(shí)就是兩個(gè)單位矢量的旋轉(zhuǎn)
然后我們使用高中學(xué)的加速度定義:加速度就是速度的變化率,即速度矢量的導(dǎo)數(shù),位移(矢徑)矢量的二階導(dǎo)數(shù)。
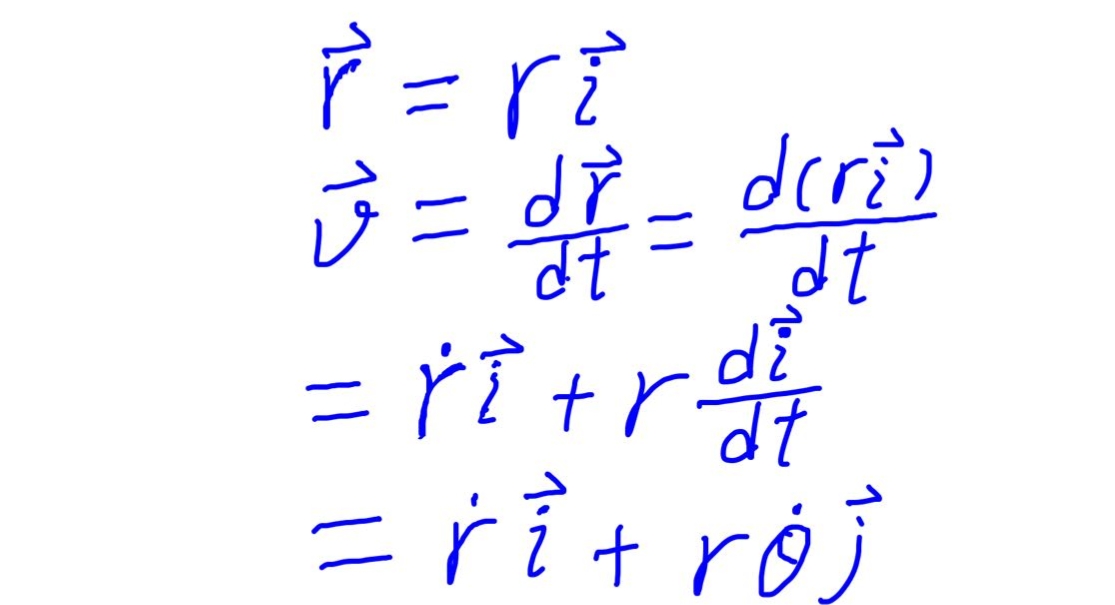

我們都知道,地球所受到的太陽(yáng)引力是徑向的,是始終指向太陽(yáng)中心的,這就決定了兩件事:第一,上式中的徑向加速度只需乘上地球質(zhì)量m就等于地球受到的引力,當(dāng)然考慮二矢量的方向剛好相反要加上負(fù)號(hào)才相等。第二,橫向加速度(注意不是切向加速度,而是與矢徑垂直的方向上的加速度)始終等于零。
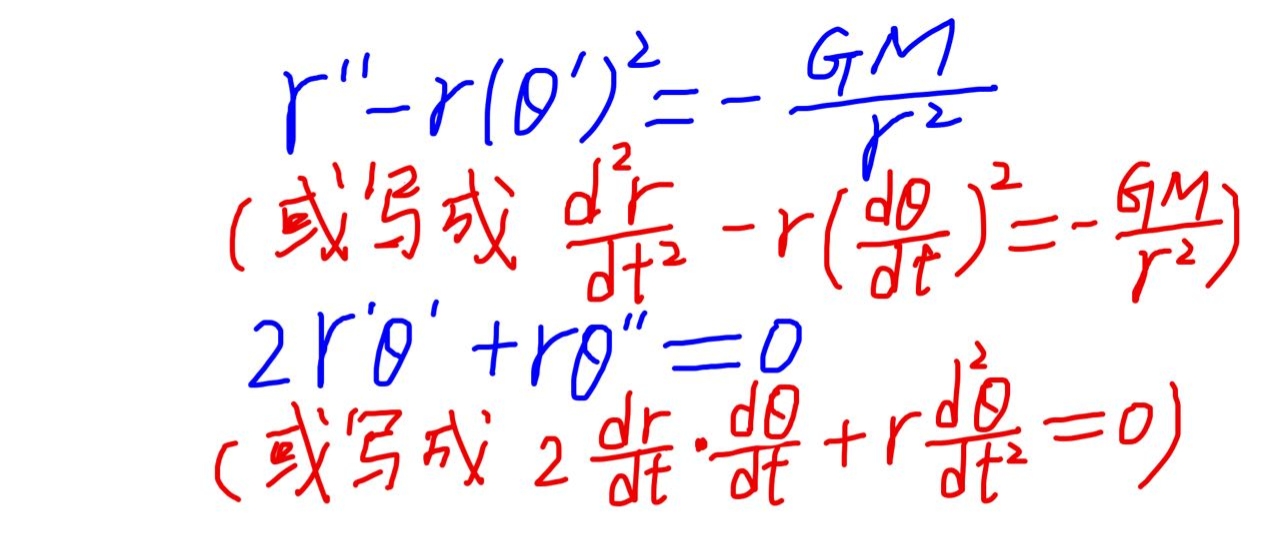
這第二項(xiàng)其實(shí)就是角動(dòng)量守恒。可以這樣證明:
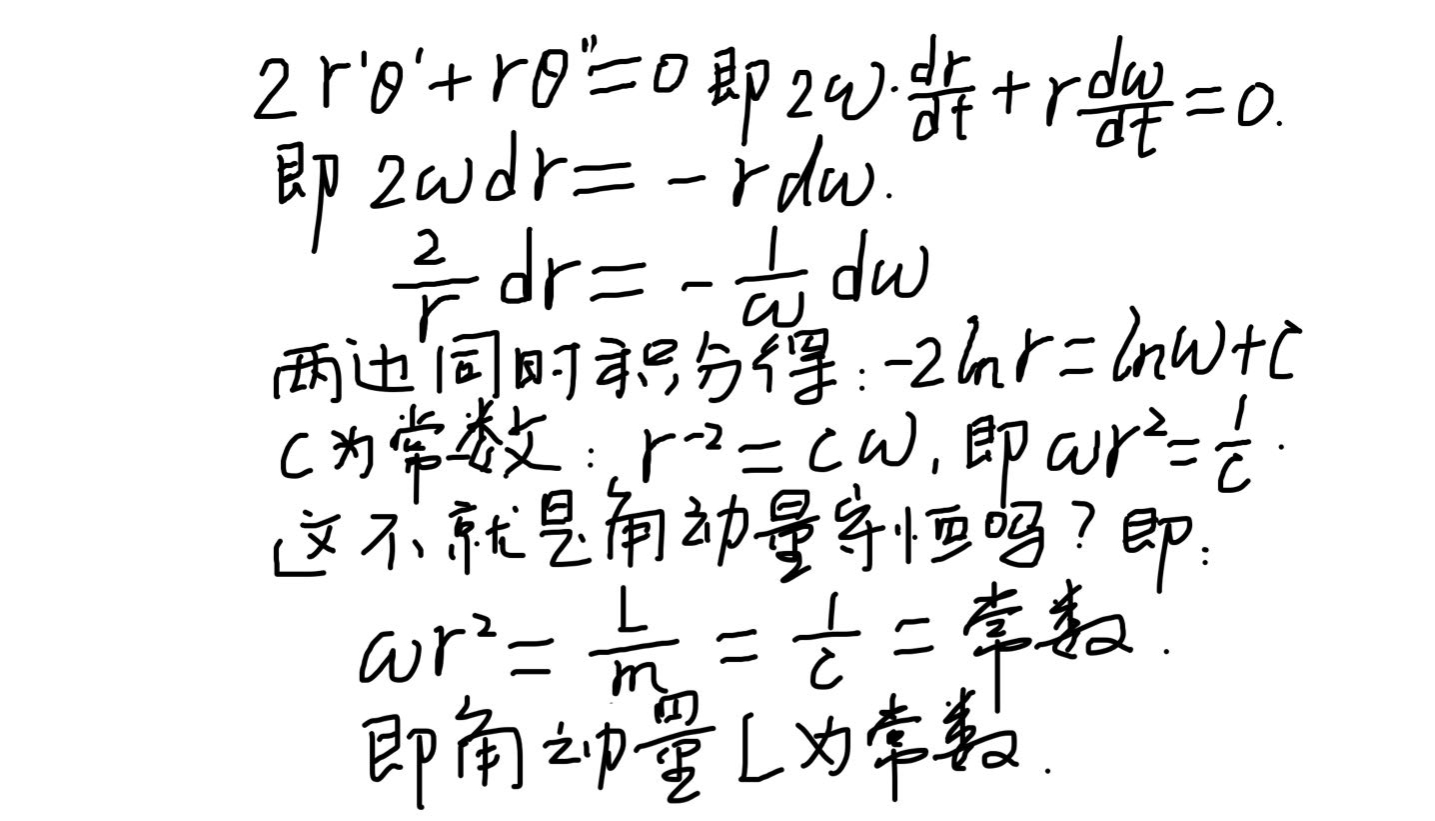
看懂這段始終要記住角速度ω等于極角θ對(duì)時(shí)間的一階導(dǎo)數(shù),ω和θ的方向都是橫向的,描述矢徑轉(zhuǎn)動(dòng)的。
接下來(lái)既然角動(dòng)量守恒,那么行星軌跡必然為一個(gè)平面:

現(xiàn)在我們已經(jīng)知道這個(gè)切向速度等于橫向速度的時(shí)刻其實(shí)就是近日點(diǎn)或遠(yuǎn)日點(diǎn)

再次證明了行星公轉(zhuǎn)運(yùn)動(dòng)的角動(dòng)量是不變的
接下來(lái)我們要想辦法求解前面寫出的徑向加速度的微分方程。

接下來(lái)就要將此式作為實(shí)質(zhì)上的r關(guān)于t的微分方程換元成為r關(guān)于θ的微分方程,得出極坐標(biāo)方程









