在機器學(xué)習(xí)和統(tǒng)計領(lǐng)域，線性回歸模型是最簡單的模型之一。這意味著，人們經(jīng)常認(rèn)為對線性回歸的線性假設(shè)不夠準(zhǔn)確。

例如，下列2個模型都是線性回歸模型，即便右圖中的線看起來并不像直線。

圖1 同一數(shù)據(jù)集的兩種不同線性回歸模型

若對此表示驚訝，那么本文值得你讀一讀。本文試圖解釋對線性回歸模型的線性假設(shè)，以及此類線性假設(shè)的重要性。

回答上述問題，需要了解以下兩個簡單例子中線性回歸逐步運行的方式。

例1：最簡單的模型

從最簡單的例子開始。給定3對（x，y）訓(xùn)練數(shù)據(jù)：（2,4）、（5,1）、（8,9）進(jìn)行函數(shù)建模，發(fā)現(xiàn)目標(biāo)變量y和輸入變量x之間的關(guān)系。

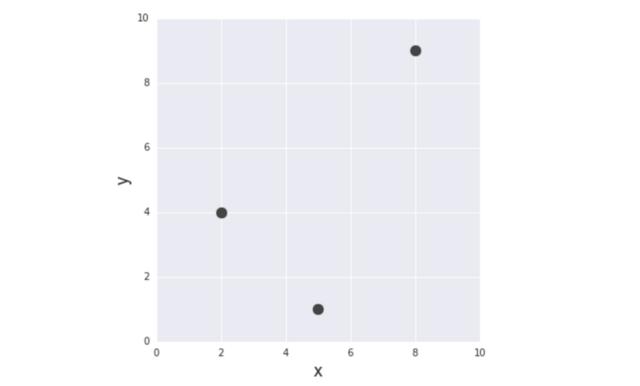
圖2 本文中使用的訓(xùn)練數(shù)據(jù)集

這一模型最為簡單，如下所示：

通過運用該簡單的線性函數(shù)，可模擬x和y之間的關(guān)系。關(guān)鍵在于該函數(shù)不僅與輸入變量x成線性關(guān)系，而且與參數(shù)a、b成線性關(guān)系。

當(dāng)前目標(biāo)是確定最符合訓(xùn)練數(shù)據(jù)的參數(shù)a和b的值。

這可通過測量每個輸入x的實際目標(biāo)值y和模型f（x）之間的失配來實現(xiàn)，并將失配最小化。這種失配（=最小值）被稱為誤差函數(shù)。

有多種誤差函數(shù)可供選擇，但其中最簡單的要數(shù)RSS，即每個數(shù)據(jù)點x對應(yīng)的模型f（x）與目標(biāo)值y的誤差平方和。

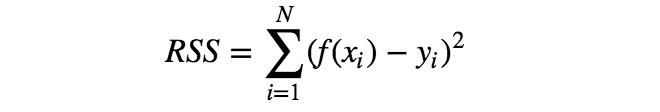
利用誤差函數(shù)的概念，可將“確定最符合訓(xùn)練數(shù)據(jù)的參數(shù)a、b”改為“確定參數(shù)a、b，使誤差函數(shù)最小化”。

計算一下訓(xùn)練數(shù)據(jù)的誤差函數(shù)。

上面的等式就是要求最小值的誤差函數(shù)。但是，怎樣才能找到參數(shù)a、b，得到此函數(shù)的最小值呢？為啟發(fā)思維，需要將該函數(shù)視覺化。

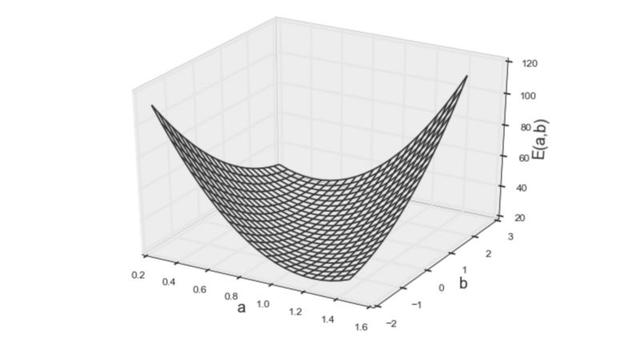
圖3 誤差函數(shù)的第一個模型

從上方的3D圖來看，人們會本能地猜測該函數(shù)為凸函數(shù)。凸函數(shù)的優(yōu)化（找到最小值）比一般數(shù)學(xué)優(yōu)化簡單得多，因為任何局部最小值都是整個凸函數(shù)的最小值。（簡單來講，就是凸函數(shù)只有一個最小點，例如“U”的形狀）由于凸函數(shù)的這種特性，通過簡單求解如下的偏微分方程，便可得到使函數(shù)最小化的參數(shù)。

下面解下之前的例子吧。

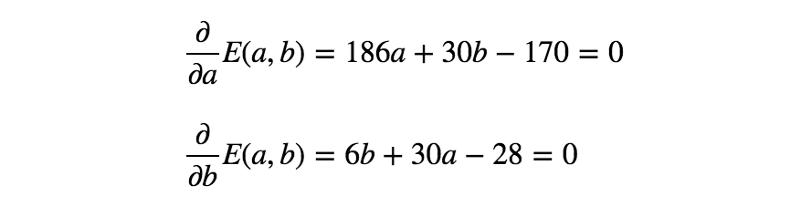
通過求解上面的等式，得到a = 5/6、b = 1/2。因此，第一個模型（最小化RSS）如下所示：

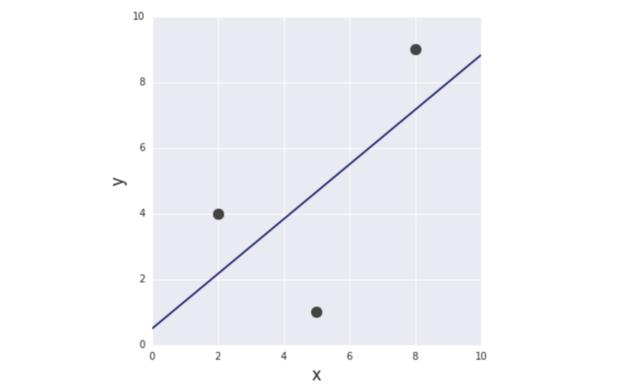
圖4 第一個模型

示例2：簡單的彎曲模型

現(xiàn)在，對于相同的數(shù)據(jù)點，可考慮如下的另一模型：

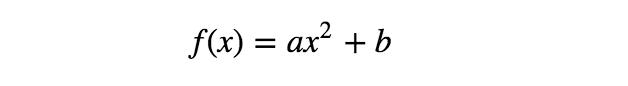
如上所示，該模型不再是輸入變量x的線性函數(shù)，但仍是參數(shù)a、b的線性函數(shù)。

下面看下這一變化對模型擬合過程的影響。我們將使用與前一示例相同的誤差函數(shù)——RSS。

如上所示，等式看起來與前一個非常相似。（系數(shù)的值不同，但方程的形式相同。）該模型的可視化圖像如下：

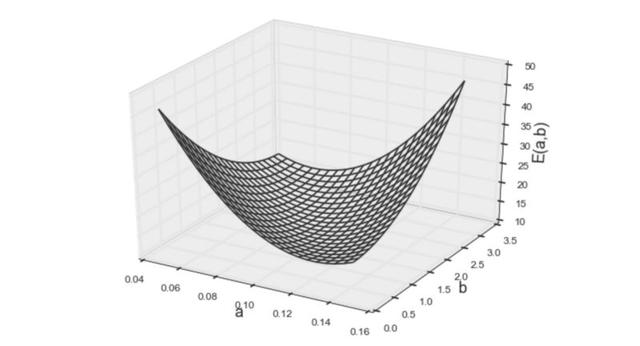
圖5 誤差函數(shù)的第二個模型

兩個模型的形狀看起來也很相似，仍然是凸函數(shù)。但秘密在于，當(dāng)使用訓(xùn)練數(shù)據(jù)計算誤差時，輸入變量作為具體值給出（例如，x²的值在數(shù)據(jù)集中給定為22、52和8²，即（2,4）、（5,1）、（8,9））。因此，無論輸入變量的形式多復(fù)雜（例如x、x²、sin（x）、log（x）等......），給定的值在誤差函數(shù)中僅為常數(shù)。

誤差函數(shù)的第二個模型也是凸函數(shù)，因此可通過與前一示例完全相同的過程找到最佳參數(shù)。

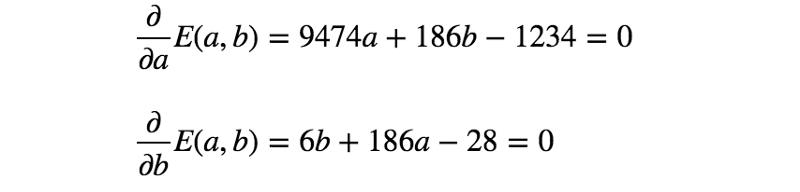
通過求解上面的等式，得到a = 61/618、b = 331/206。所以，第二個模型如下所示：

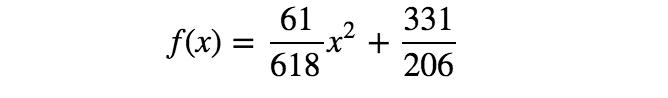
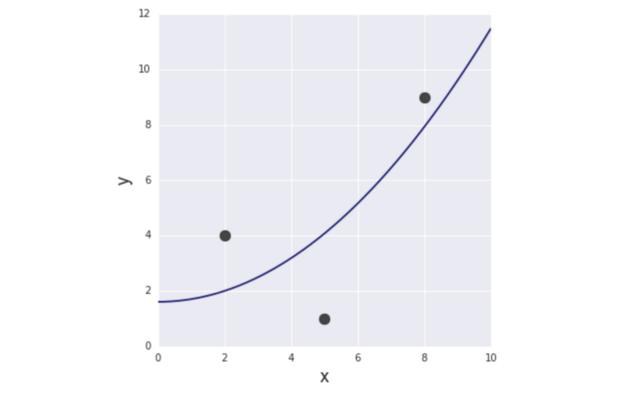
圖6 第二個模型

結(jié)論：線性回歸模型的線性假設(shè)

上述2個例子的求解過程完全相同（且非常簡單），即使一個為輸入變量x的線性函數(shù)，一個為x的非線性函數(shù)。兩個模型的共同特征是兩個函數(shù)都與參數(shù)a、b成線性關(guān)系。這是對線性回歸模型的線性假設(shè)，也是線性回歸模型數(shù)學(xué)單性的關(guān)鍵。

上面2個模型非常簡單，但一般而言，模型與其參數(shù)的線性假設(shè)，可保證RSS始終為凸函數(shù)。通過求解簡單偏微分方程，得到最優(yōu)參數(shù)，這就是線性假設(shè)至關(guān)重要的原因。