俗話說(shuō)“一圖勝千言”。通過各種圖片和圖形化展示,我們可以更清晰地表達(dá)很多抽象概念、理論、數(shù)據(jù)模式或某些想法。在本章中,我們首先解釋為什么應(yīng)該關(guān)心數(shù)據(jù)可視化。然后,我們將討論幾種在R、Python和Julia中常用的數(shù)據(jù)可視化技術(shù)。此外,我們還將介紹幾個(gè)特殊主題,例如如何生成圖形、餅圖和條形圖,如何添加標(biāo)題、趨勢(shì)線、希臘字母,以及如何輸出圖形。在本章的最后,我們將討論一個(gè)可選話題,即動(dòng)態(tài)表示以及如何將它們保存為html文件。
本章包含以下主題:
- 數(shù)據(jù)可視化的重要性
- R數(shù)據(jù)可視化
- Python數(shù)據(jù)可視化
- Julia數(shù)據(jù)可視化
4.1 數(shù)據(jù)可視化的重要性
對(duì)于數(shù)據(jù)科學(xué)和商業(yè)分析領(lǐng)域的用戶或研究人員來(lái)說(shuō),使用各種類型的圖形、餅圖、條形圖以及其他視覺手段展示數(shù)據(jù)中隱含的潛在趨勢(shì)或模式對(duì)理解數(shù)據(jù)至關(guān)重要,同時(shí)能夠幫助研究人員更好地向觀眾或客戶呈現(xiàn)數(shù)據(jù)。這樣做主要有以下幾個(gè)原因。
第一,語(yǔ)言有時(shí)很難描述我們的發(fā)現(xiàn),尤其是存在幾種模式或諸多影響因素時(shí),通過幾個(gè)單獨(dú)的圖形和一個(gè)連接圖則可以更好地理解和解釋復(fù)雜的關(guān)系。
第二,我們可以使用圖形或圖片來(lái)解釋某些算法,例如二分法(參見4.9節(jié))。
第三,我們也可以使用相對(duì)大小來(lái)表示不同的含義。在金融領(lǐng)域,一個(gè)基本概念叫作貨幣時(shí)間價(jià)值(Time Value of Money,TVM),意思是“一鳥在手勝過雙鳥在林”。今天的100美元比同等數(shù)額的未來(lái)現(xiàn)金流更有價(jià)值。通過不同尺寸的不同圓圈表示發(fā)生在未來(lái)不同時(shí)間點(diǎn)上的現(xiàn)金流的現(xiàn)值,可以幫助讀者更清楚地理解這個(gè)概念。
第四,我們的數(shù)據(jù)可能非常混亂,所以簡(jiǎn)單地展示數(shù)據(jù)點(diǎn)可能會(huì)使讀者更加困惑。如果我們能用一個(gè)簡(jiǎn)單的圖形來(lái)展示它的主要特征、屬性或模式將大有益處。
4.2 R數(shù)據(jù)可視化
首先,我們來(lái)看R中最簡(jiǎn)單的圖形。利用下面一行R代碼,我們畫出了從
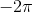
到

范圍內(nèi)的余弦函數(shù)值:
> plot(cos,-2*pi,2*pi)
對(duì)應(yīng)的圖形如圖4.1所示。

圖4.1 余弦函數(shù)圖
直方圖也有助于我們理解數(shù)據(jù)點(diǎn)的分布。圖4.1就是一個(gè)簡(jiǎn)單的例子。首先,我們生成一組服從標(biāo)準(zhǔn)正態(tài)分布的隨機(jī)數(shù)。為了便于說(shuō)明,第一行的set.seed()命令其實(shí)是多余的,它的存在將保證所有使用相同seed值(本例中為333)的用戶將得到相同的隨機(jī)數(shù)集合。
換句話說(shuō),在輸入值相同的情況下,直方圖看起來(lái)將是一樣的。在下一行中,rnorm(n)函數(shù)畫出了n個(gè)服從標(biāo)準(zhǔn)正態(tài)分布的隨機(jī)數(shù)。接著,最后一行使用hist()函數(shù)生成一個(gè)直方圖:
> set.seed(333)
> data<-rnorm(5000)
> hist(data)
相關(guān)直方圖如圖4.2所示。

圖4.2 示例直方圖
注意,代碼rnorm(5000)與rnorm(5000,mean=0,sd=1)相同,其中含義為均值的默認(rèn)值為0,sd的默認(rèn)值為1。下一個(gè)R程序?qū)闃?biāo)準(zhǔn)正態(tài)分布左側(cè)的尾巴填充陰影:
x<-seq(-3,3,length=100)
y<-dnorm(x,mean=0,sd=1)
title<-"Area under standard normal dist & x less than -2.33"
yLabel<-"standard normal distribution"
xLabel<-"x value"
plot(x,y,type="l",lwd=3,col="black",main=title,xlab=xLabel,ylab=yLabel)
x<-seq(-3,-2.33,length=100)
y<-dnorm(x,mean=0,sd=1)
polygon(c(-4,x,-2.33),c(0,y,0),col="red")
相關(guān)圖形如圖4.3所示。

圖4.3 標(biāo)準(zhǔn)正態(tài)分布示例圖
注意,根據(jù)上面代碼中的最后一行可知,陰影區(qū)域?yàn)榧t色。
在探索各種數(shù)據(jù)集的屬性方面,R包rattle非常有用。如果rattle包沒有預(yù)先安裝,那么我們可以運(yùn)行以下代碼安裝它:
> install.packages("rattle")
然后,運(yùn)行以下代碼啟動(dòng)它:
> library(rattle)
> rattle()
單擊回車鍵后,可以看到圖4.4中的結(jié)果。

圖4.4 Rattle包啟動(dòng)界面
首先,我們需要導(dǎo)入某些數(shù)據(jù)集。我們從7種可能的格式中選擇數(shù)據(jù)源,如文件、 ARFF、ODBC、R數(shù)據(jù)集和RData文件,并且可以從此處加載數(shù)據(jù)。
最簡(jiǎn)單的方法是使用Library選項(xiàng),它將列出rattle包中所有內(nèi)嵌的數(shù)據(jù)集。單擊Library后,我們可以看到內(nèi)嵌數(shù)據(jù)集的列表。假設(shè)單擊左上角的Execute后我們選擇了acme:boot:Monthly Excess Returns,那么我們將看到圖4.5中的界面。

圖4.5 導(dǎo)入數(shù)據(jù)集界面
現(xiàn)在,我們就可以研究數(shù)據(jù)集的屬性了。點(diǎn)擊Explore后,我們可以使用各種圖形來(lái)查看數(shù)據(jù)集。假設(shè)我們選擇Distribution,并勾選Benford復(fù)選框,那么我們就可以參考圖4.6來(lái)了解更多細(xì)節(jié)。

圖4.6 查看數(shù)據(jù)集屬性信息
單擊Execute之后,將彈出圖4.7所示內(nèi)容。圖4.7上方的紅線顯示了根據(jù)本福特定律(Benford Law)算出的1~9每個(gè)數(shù)字的頻率,而底部的藍(lán)線則展示了數(shù)據(jù)集的屬性。請(qǐng)注意,如果你的計(jì)算機(jī)系統(tǒng)中還沒有安裝reshape包,則此命令要么無(wú)法運(yùn)行,要么會(huì)請(qǐng)求許可將該包安裝到你的計(jì)算機(jī)上。

圖4.7 數(shù)據(jù)集的Benford定律符合情況
在圖4.7中,兩條線之間的巨大差異表明我們的數(shù)據(jù)不符合本福特定律建議的分布規(guī)律。在現(xiàn)實(shí)世界中,我們知道很多人、事件和經(jīng)濟(jì)活動(dòng)是相互關(guān)聯(lián)的,使用各種圖形來(lái)展示這樣一個(gè)多節(jié)點(diǎn)、相互連接的圖像是一個(gè)很好的辦法。如果沒有預(yù)裝qgraph包,那么用戶必須運(yùn)行以下程序來(lái)安裝它:
> install.packages("qgraph")
下一個(gè)程序展示了從a到b、a到c等節(jié)點(diǎn)之間的連接:
library(qgraph)
stocks<-c("IBM","MSFT","WMT")
x<-rep(stocks, each = 3)
y<-rep(stocks, 3)
correlation<-c(0,10,3,10,0,3,3,3,0)
data <- as.matrix(data.frame(from =x, to =y, width =correlation))
qgraph(data, mode = "direct", edge.color = rainbow(9))
如果將數(shù)據(jù)展示出來(lái),該程序的意義就會(huì)更加清晰。相關(guān)性展示出這些股票之間聯(lián)系的緊密程度。注意,所有這些值都是隨機(jī)選擇的,并沒有現(xiàn)實(shí)意義。
> data
from to width
[1,] "IBM" "IBM" " 0"
[2,] "IBM" "MSFT" "10"
[3,] "IBM" "WMT" " 3"
[4,] "MSFT" "IBM" "10"
[5,] "MSFT" "MSFT" " 0"
[6,] "MSFT" "WMT" " 3"
[7,] "WMT" "IBM" " 3"
[8,] "WMT" "MSFT" " 3"
[9,] "WMT" "WMT" " 0"
第3個(gè)變量的值越大表明前面兩個(gè)變量的相關(guān)性越強(qiáng)。例如,IBM與MSFT的相關(guān)性更強(qiáng)(值為10),大于IBM與WMT的相關(guān)性(值為3)。圖4.8展示了這3只股票的相關(guān)性強(qiáng)弱程度。

圖4.8 IBM、MSFT和WMT股票的相關(guān)性強(qiáng)弱程度
以下程序展示了5個(gè)因素之間的關(guān)系或相互聯(lián)系:
library(qgraph)
data(big5)
data(big5Groups)
title("Correlations among 5 factors",line = 2.5)
qgraph(cor(big5),minimum = 0.25,cut = 0.4,vsize = 1.5,
groups = big5groups,legend = TRUE, borders = FALSE,theme = 'gray')
相關(guān)圖形如圖4.9所示。

圖4.9 5個(gè)因素之間的相互聯(lián)系
4.3 Python數(shù)據(jù)可視化
Python中圖形和圖像方面使用最廣泛的包是matplotlib。下面的程序僅僅包含3行代碼,所以可以看作是最簡(jiǎn)單的生成一個(gè)圖形的Python程序:
import matplotlib.pyplot as plt
plt.plot([2,3,8,12])
plt.show()
第一行命令會(huì)上傳一個(gè)名為matplotlib.pyplot的Python包,并將其重命名為plt。
注意,我們甚至可以使用其他簡(jiǎn)短的名稱,但通常使用plt表示matplotlib包。第二行繪制了4個(gè)點(diǎn),最后一行總結(jié)了整個(gè)過程。完整圖形如圖4.10所示。
在下一個(gè)例子中,我們?yōu)閤和y添加了標(biāo)簽,以及一個(gè)標(biāo)題。所使用的函數(shù)是余弦函數(shù),其中輸入值范圍為

~

。
import scipy as sp
import matplotlib.pyplot as plt
x=sp.linspace(-2*sp.pi,2*sp.pi,200,endpoint=True)
y=sp.cos(x)
plt.plot(x,y)
plt.xlabel("x-value")
plt.ylabel("Cosine function")
plt.title("Cosine curve from -2pi to 2pi")
plt.show()
圖4.10 matplotlib包生成的圖形示例
漂亮的余弦曲線如圖4.11所示。
如果我們今天收到100美元,它將比兩年后收到的更有價(jià)值,這個(gè)概念叫作貨幣時(shí)間價(jià)值,因?yàn)槲覀儸F(xiàn)在可以將100美元存入銀行來(lái)賺取利息。下面的Python程序使用size來(lái)說(shuō)明此概念。
import matplotlib.pyplot as plt
fig = plt.figure(facecolor='white')
dd = plt.axes(frameon=False)
dd.set_frame_on(False)
dd.get_xaxis().tick_bottom()
dd.axes.get_yaxis().set_visible(False)
x=range(0,11,2)
x1=range(len(x),0,-1)
y = [0]*len(x);
plt.annotate("$100 received
today",xy=(0,0),xytext=(2,0.15),arrowprops=dict(facecolor='black',shrink=2))
plt.annotate("$100 received in 2
years",xy=(2,0),xytext=(3.5,0.10),arrowprops=dict(facecolor='black',shrink=
2))
s = [50*2.5**n for n in x1];
plt.title("Time value of money ")
plt.xlabel("Time (number of years)")
plt.scatter(x,y,s=s);
plt.show()
圖4.11 為圖形添加x和y軸標(biāo)簽及標(biāo)題
相關(guān)的圖形如圖4.12所示。同樣,不同尺寸表示它們現(xiàn)值的相對(duì)大小。

圖4.12 貨幣時(shí)間價(jià)值概念解釋
4.4 Julia數(shù)據(jù)可視化
對(duì)于下面的Julia程序,我們使用了一個(gè)名為Plots的包,用于安裝此包的命令為Pkg.add("Plots")。這里,我們通過一個(gè)Jupyter notebook運(yùn)行Julia程序。圖4.13展示了一個(gè)Julia程序。

圖4.13 Julia程序
單擊菜單欄上的Kernel項(xiàng)目,然后單擊Restart and Run All,我們得到圖4.14所示的結(jié)果。

圖4.14 運(yùn)行結(jié)果圖
同樣地,srand(123)命令保證使用相同隨機(jī)種子的任何用戶都會(huì)得到相同的隨機(jī)數(shù)集合。為此,用戶會(huì)得到與前面相同的圖形。下一個(gè)例子是使用Julia包PyPlot繪制的散點(diǎn)圖。
using PyPlot
n=50
srand(333)
x = 100*rand(n)
y = 100*rand(n)
areas = 800*rand(n)
fig = figure("pyplot_scatterplot",figsize=(10,10))
ax = axes()
scatter(x,y,s=areas,alpha=0.5)
title("using PyPlot: Scatter Plot")
xlabel("X")
ylabel("Y")
grid("on")
相關(guān)圖形如圖4.15所示。

圖4.15 Julia包PyPlot繪制散點(diǎn)圖示例
下一個(gè)Julia程序借鑒自Sargent和Stachurski的程序。
using QuantEcon: meshgrid
using PyPlot:surf
using Plots
n = 50
x = linspace(-3, 3, n)
y = x
z = Array{Float64}(n, n)
f(x, y) = cos(x^2 + y^2) / (1 + x^2 + y^2)
for i in 1:n
for j in 1:n
z[j, i] = f(x[i], y[j])
end
end
xgrid, ygrid = meshgrid(x, y)
surf(xgrid, ygrid, z',alpha=0.7)
令人印象深刻的圖形如圖4.16所示。

圖4.16 Sargent和Stachurski程序結(jié)果圖
本文截選自:《Anaconda數(shù)據(jù)科學(xué)實(shí)戰(zhàn)》






