你想用深度學習譜寫自己的音樂嗎？這篇指南來幫助你！（附代碼）-魔扣目錄

作者：ARAVIND PAI

翻譯：吳金笛

校對：和中華

本文長度為6800字，建議閱讀15分鐘

本文手把手帶你使用Python編寫一個自動生成音樂的模型。

總覽

學習如何開發一個自動生成音樂的端到端模型
理解WaveNet架構并使用Keras從零開始實現它
在建立自動音樂生成模型的同時，比較了WaveNet和Long-Short-Term Memory的性能

介紹

“如果我不是物理學家，我可能會成為音樂家。我經常在音樂中思考。我活在音樂的白日夢里。我從音樂的角度來看待我的生活。”——阿爾伯特·愛因斯坦

我可能不是愛因斯坦先生那樣的物理學家，但我完全同意他對音樂的看法!我不記得有哪一天我沒有打開音樂播放器。我上下班都伴隨著音樂的旋律，老實說，它幫助我專注于工作。

我一直夢想著作曲，但卻不懂樂器。直到我遇到了深度學習，這一切都成了過去。使用某些技術和框架，我能夠在不了解任何樂理的情況下創作自己的原創音樂樂譜!

這是我最喜歡的專業項目之一。我結合了兩個愛好——音樂和深度學習——創建了一個自動的音樂生成模型。夢想成真了!

我很高興與你分享我的方法，包括使你也能夠生成原創音樂的全部代碼!首先，我們將快速理解自動音樂生成的概念，然后再深入了解用于執行此操作的不同方法。最后，我們將啟用Python并設計我們自己的自動音樂生成模型。

1. 什么是音樂自動生成？

2. 音樂的組成要素是什么？

3. 生成音樂的不同方法

使用WaveNet架構
使用Long-Short-Term Memory（LSTM）

4. 實現——使用python進行自動作曲

什么是音樂自動生成？

“音樂是一種藝術，是一種通用的語言。”

我把音樂定義為不同頻率的音調的集合。因此，自動音樂生成是一個用最少的人為干預來創作一首短曲的過程。

產生音樂最簡單的形式是什么?

這一切都是從隨機選擇聲音并將它們組合成一段音樂開始的。1787年，莫扎特為這些隨機聲音的選擇提出了骰子游戲。他手動合成了近272個音調!然后，他根據兩個骰子點數之和選擇一個音調。

另一個有趣的想法是利用音樂語法來生成音樂。

“音樂語法是指對音樂聲音的合理安排和組合以及對音樂作品的正確表現所必需的知識”

-《音樂語法基礎》

在20世紀50年代早期，Iannis Xenakis使用統計學和概率的概念來創作音樂——通常被稱為隨機音樂(Stochastic Music)。他將音樂定義為偶然出現的一系列元素(或聲音)。因此，他用隨機理論來表述它。他對元素的隨機選擇完全依賴于數學概念。

最近，深度學習架構已經成為自動音樂生成的最新技術。在本文中，我將討論使用WaveNet和LSTM(Long-Short-Term Memory)架構來實現自動作曲的兩種不同方法。

注意:本文需要對一些深度學習概念有基本的理解。我建議閱讀以下文章:

從頭開始學習卷積神經網絡(CNNs)的全面教程

https://www.analyticsvidhya.com/blog/2018/12/guide-convolutional-neural-network-cnn/?utm_source=blog&utm_medium=how-to-perform-automatic-music-generation

深度學習要領:長短期記憶(LSTM)入門

https://www.analyticsvidhya.com/blog/2017/12/fundamentals-of-deep-learning-introduction-to-lstm/?utm_source=blog&utm_medium=how-to-perform-automatic-music-generation

學習序列建模的必讀教程

https://www.analyticsvidhya.com/blog/2019/01/sequence-models-deeplearning/?utm_source=blog&utm_medium=how-to-perform-automatic-music-generation

音樂的組成要素是什么?

音樂本質上是由音符和和弦組成的。讓我從鋼琴的角度來解釋這些術語:

音符：單鍵發出的聲音稱為音符
和弦：由兩個或更多的鍵同時發出的聲音稱為和弦。一般來說，大多數和弦包含至少3個鍵音
八度：重復的模式稱為八度。每個八度包含7個白鍵和5個黑鍵

自動生成音樂的不同方法

我將詳細討論兩個基于深度學習的自動生成音樂的架構——WaveNet和LSTM。但是，為什么只有深度學習架構?

深度學習是一個受神經結構啟發的機器學習領域。這些網絡自動從數據集中提取特征，并能夠學習任何非線性函數。這就是為什么神經網絡被稱為泛函逼近器（感覺泛函在數學上的定義不適合這里，網上也有人翻譯為萬能函數擬逼近器，因為最早有一篇關于 Universal Approximation Theorem的論文）。

因此，深度學習模型是自然語言處理(NLP)、計算機視覺、語音合成等各個領域的最新技術。讓我們來看看如何構建這些作曲模型。

方法一：使用WaveNet

“WaveNet是谷歌DeepMind開發的一種基于深度學習的原始音頻生成模型。”

WaveNet的主要目的是從原始的數據分布中生成新的樣本。因此，它被稱為生成模型。

“WaveNet就像是NLP中的一種語言模型。”

在語言模型中，給定一個單詞序列，該模型試圖預測下一個單詞。與語言模型類似，在WaveNet中，給定一系列樣本，它試圖預測下一個樣本。

方法二：使用Long-Short-Term Memory（LSTM）模型

Long-Short-Term Memory (LSTM)是遞歸神經網絡(RNNs)的一種變體，能夠捕獲輸入序列中的長期依賴關系。LSTM在序列到序列(Seq2Seq)建模任務中有廣泛的應用，如語音識別、文本摘要、視頻分類等。

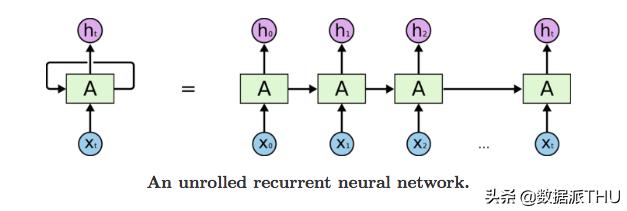
讓我們詳細討論如何使用這兩種方法訓練我們的模型。

WaveNet：訓練階段

“這是一個多對一的問題，其中輸入是一系列振幅值，輸出是后續值。”

讓我們看看如何準備輸入和輸出序列。

WaveNet的輸入:

WaveNet將原始音頻波的小塊作為輸入。原始音頻波是指波在時間序列域中的表示。

在時間序列域中，音頻波以不同時間間隔音符的振幅值的形式表示:

WaveNet的輸出:

給定振幅值的序列，WaveNet試圖預測連續的振幅值。

讓我們通過一個示例來理解。考慮一個5秒的音頻波，采樣率為16,000(即每秒16,000個樣本)。現在，我們有8萬個樣本在5秒內以不同的時間間隔記錄下來。讓我們把音頻分成相同大小的塊，比如1024(這是一個超參數)。

下圖展示了模型的輸入和輸出序列:

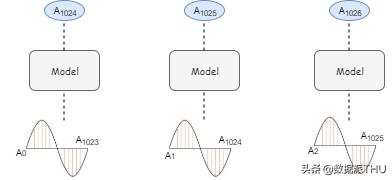
前3個塊的輸入和輸出

對于其余的塊，我們可以遵循類似的過程。

從上面我們可以推斷出，每個塊的輸出只依賴于過去的信息(即以前的時間步長)，而不依賴于未來的時間步長。因此，該任務稱為自回歸任務，該模型稱為自回歸模型。

推理階段

在推理階段，我們將嘗試生成新的樣本。讓我們看看怎么做:

1. 選擇一個隨機的樣本值數組作為建模的起點

2. 現在，模型輸出所有樣本的概率分布

3. 選擇概率最大的值并將其追加到先前的樣本值數組中

4. 刪除第一個元素并作為下一個迭代的輸入傳入模型

5. 重復步驟2和4，進行一定次數的迭代

理解WaveNet架構

WaveNet的基本結構是因果擴散的一維卷積層。首先讓我們了解相關概念的重要性。

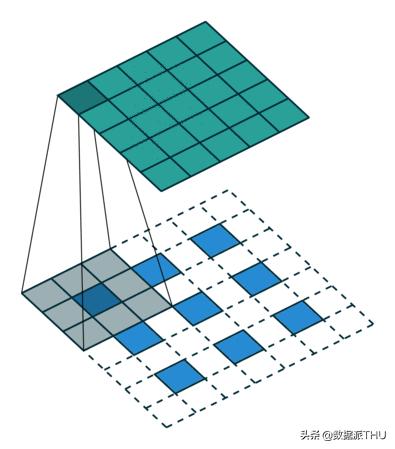
為什么使用卷積，什么是卷積?

“使用卷積的一個主要原因是從輸入中提取特征。”

例如，在圖像處理的情況下，用過濾器對圖像進行卷積可以得到一個特征圖。

卷積是一種結合了兩個函數的數學運算。在圖像處理的情況下，卷積是圖像的某些部分與核(kernel)的線性組合。

你可以瀏覽下面的文章閱讀更多關于卷積的知識:

卷積神經網絡(CNNs)結構的解密

https://www.analyticsvidhya.com/blog/2017/06/architecture-of-convolutional-neural-networks-simplified-demystified/?utm_source=blog&utm_medium=how-to-perform-automatic-music-generation

什么是一維卷積？

一維卷積的目標類似于長短期記憶模型。它用于解決類似于LSTM的任務。在一維卷積中，核或者叫過濾器只沿著一個方向運動:

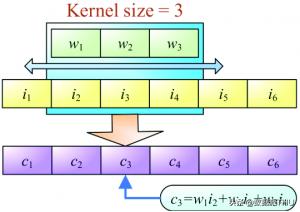
卷積的輸出取決于核的大小、輸入形狀、填充類型和步長。現在，我將帶領你們了解不同類型的填充來理解使用擴張的1D因果卷積層的重要性。

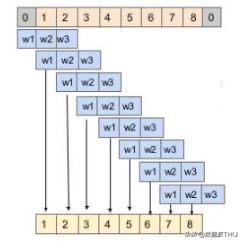
當我們將填充設置為valid時，輸入和輸出序列的長度會發生變化。輸出長度小于輸入長度:

當我們將填充設置為same時，在輸入序列的兩側填充零以使輸入和輸出的長度相等：

一維卷積的優點:

捕獲輸入序列中出現的序列信息
與GRU或LSTM相比，訓練的速度要快得多，因為它們沒有循環性的連接

一維卷積的缺點:

當填充設置為same時，在時間步長t處的輸出也與之前的t-1和未來的時間步長t+1進行卷積。因此，它違反了自回歸原則
當填充被設置為valid時，輸入和輸出序列的長度會發生變化，這是計算殘差連接所需要的(后面會講到)

這為因果卷積掃清了道路。

注意: 我在這里提到的利弊是針對于此問題的。

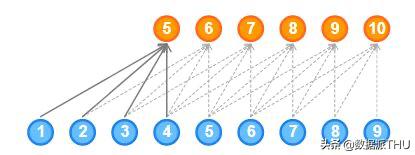
什么是一維因果卷積?

它被定義為這樣一種卷積，即t時刻的輸出僅與t時刻以及前一層更早的元素進行卷積。

簡單地說，正常卷積和因果卷積的區別僅僅在于填充。在因果卷積中，僅在輸入序列的左邊加0，以保持自回歸的原則:

因果一維卷積的優點:

因果卷積沒有考慮未來的時間步長，而這是建立生成模型的一個標準

因果一維卷積的缺點:

因果卷積不能回溯到序列中過去發生的時間步長。因此，因果卷積的接受域非常低。網絡的接受域是指影響輸出的輸入數量:

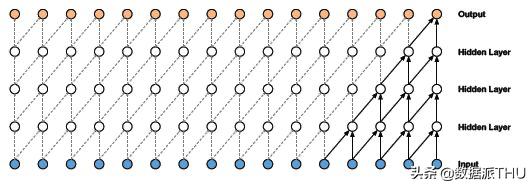
如你所見，輸出只受5個輸入的影響。因此，網絡的接受域為5，非常低。網絡的接受域也可以通過增加大尺寸的核來增加，但是要記住，這樣一來計算復雜度也會增加。

這將為我們引出擴張一維因果卷積的絕佳概念。

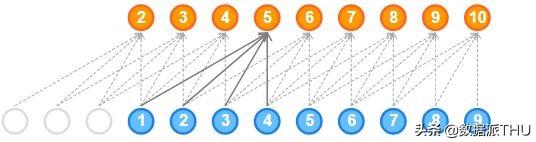
什么是擴張一維因果卷積?

“在核的值之間有孔或空缺的因果一維卷積層稱為擴張的一維卷積。”

所增加的空缺數由擴張率決定。它定義了網絡的接受域。大小為k、擴張率為d的核在核k的每個值之間都有d-1個孔。

如你所見，將一個3 * 3的核與一個7 * 7的輸入，以擴張率為2進行卷積，最終接受域為5 * 5。

擴張一維因果卷積的優點:

擴張的一維卷積網絡通過指數增加每一隱藏層的擴張率來增加接受域:

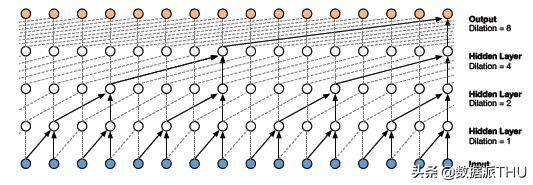
如你所見，輸出受所有輸入的影響。因此，網絡的接受域為16。

WaveNet的殘差塊:

為了加速模型的收斂，添加了殘差連接和跳躍連接的構件:

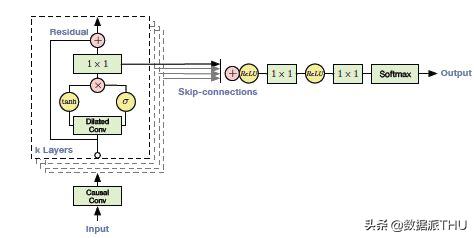
WaveNet的工作流程:

輸入進入一個因果一維卷積
輸出然后進入到2個不同的擴張一維卷積層并使用sigmoid和tanh激活
兩個不同激活值逐元素相乘導致跳躍連接
而跳躍連接和因果一維輸出的逐元素相加會導致殘差

Long Short Term Memory (LSTM)方法

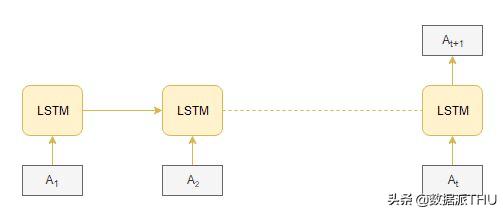
另一種自動生成音樂的方法是基于長短期記憶(LSTM)模型。輸入和輸出序列的準備類似于WaveNet。在每一個時間步長，一個振幅值被輸入到長短期記憶單元-然后它計算隱藏的向量，并把它傳遞到下一個時間步。

基于當前的輸入a（t）和先前的隱藏向量h（t-1）來計算當前時間的隱藏向量h（t）。序列信息在任何循環（一般recursive會翻譯為遞歸）神經網絡中都是這樣捕獲的:

LSTM的優點:

捕獲輸入序列中出現的順序信息

LSTM的缺點:

由于它是按順序處理輸入信息的，所以它在訓練上會花費大量的時間

實現-使用Python進行自動音樂生成

等待結束了!讓我們開發一個用于自動生成音樂的端到端模型。啟動你的Jupyter

notebook或Colab(或任何你喜歡的IDE)。

下載數據集:

我從眾多資源中下載并組合了多個數字鋼琴(譯者注：Digital piano與電鋼琴Electric Piano的區別在于音源的產生方式)的古典音樂文件。你可以從這里下載最終的數據集。

（https://drive.google.com/file/d/1qnQVK17DNVkU19MgVA4Vg88zRDvwCRXw/view）

導入庫:

Music 21是MIT開發的用于理解音樂數據的Python庫。MIDI是存儲音樂文件的一種標準格式。MIDI代表樂器數字接口。MIDI文件包含說明而不是實際的音頻。因此，它只占用很少的內存。這就是為什么它在傳輸文件時通常是首選的。

1. #library for understanding music  2. from music21 import *

讀取音樂文件：

我們直接定義一個函數來讀取MIDI文件。它返回音樂文件中存在的音符和和弦的數組。

1. #defining function to read MIDI files  2. def read_midi(file):  3.       4.     print("Loading Music File:",file)  5.       6.     notes=[]  7.     notes_to_parse = None  8.       9.     #parsing a midi file  10.     midi = converter.parse(file)  11.     12.     #grouping based on different instruments  13.     s2 = instrument.partitionByInstrument(midi)  14.   15.     #Looping over all the instruments  16.     for part in s2.parts:  17.       18.         #select elements of only piano  19.         if 'Piano' in str(part):   20.           21.             notes_to_parse = part.recurse()   22.         23.             #finding whether a particular element is note or a chord  24.             for element in notes_to_parse:  25.                   26.                 #note  27.                 if isinstance(element, note.Note):  28.                     notes.append(str(element.pitch))  29.                   30.                 #chord  31.                 elif isinstance(element, chord.Chord):  32.                     notes.append('.'.join(str(n) for n in element.normalOrder))  33.   34.     return np.array(notes)

現在，將MIDI文件加載到我們的環境中

1. #for listing down the file names  2. import os  3.   4. #Array Processing  5. import numpy as np  6.   7. #specify the path  8. path='schubert/'  9.   10. #read all the filenames  11. files=[i for i in os.listdir(path) if i.endswith(".mid")]  12.   13. #reading each midi file  14. notes_array = np.array([read_midi(path+i) for i in files])

理解數據：

在本節中，我們將探索數據集并對其進行詳細了解。

1. #converting 2D array into 1D array  2. notes_ = [element for note_ in notes_array for element in note_]  3.   4. #No. of unique notes  5. unique_notes = list(set(notes_))  6. print(len(unique_notes))

輸出：304

如你所這里見，不重復音符的數量是304。現在，讓我們看一下音符的分布。

1. #importing library  2. from collections import Counter  3.   4. #computing frequency of each note  5. freq = dict(Counter(notes_))  6.   7. #library for visualiation  8. import matplotlib.pyplot as plt  9.   10. #consider only the frequencies  11. no=[count for _,count in freq.items()]  12.   13. #set the figure size  14. plt.figure(figsize=(5,5))  15.   16. #plot  17. plt.hist(no)

輸出：

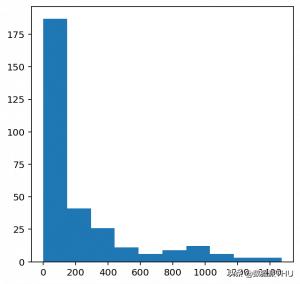
從上圖可以看出，大多數音符的頻率都很低。因此，我們保留最常用的音符，而忽略低頻率的音符。在這里，我將閾值定義為50。不過，這個參數是可以更改的。

1. frequent_notes = [note_ for note_, count in freq.items() if count>=50]  2. print(len(frequent_notes))

輸出：167

如你在這里看到的，經常出現的音符大約有170個。現在，讓我們準備新的音樂文件，其中僅包含最常見的音符

1. new_music=[]  2.   3. for notes in notes_array:  4.     temp=[]  5.     for note_ in notes:  6.         if note_ in frequent_notes:  7.             temp.append(note_)              8.     new_music.append(temp)  9.       10. new_music = np.array(new_music)

準備數據：

如文章中所述準備輸入和輸出序列：

1. no_of_timesteps = 32  2. x = []  3. y = []  4.   5. for note_ in new_music:  6.     for i in range(0, len(note_) - no_of_timesteps, 1):  7.           8.         #preparing input and output sequences  9.         input_ = note_[i:i + no_of_timesteps]  10.         output = note_[i + no_of_timesteps]  11.           12.         x.append(input_)  13.         y.append(output)  14.           15. x=np.array(x)  16. y=np.array(y)

現在，我們將為每個音符分配一個唯一的整數：

1. unique_x = list(set(x.ravel()))  2. x_note_to_int = dict((note_, number) for number, note_ in enumerate(unique_x))

我們將為輸入數據準備整數序列

1. #preparing input sequences  2. x_seq=[]  3. for i in x:  4.     temp=[]  5.     for j in i:  6.         #assigning unique integer to every note  7.         temp.append(x_note_to_int[j])  8.     x_seq.append(temp)  9.       10. x_seq = np.array(x_seq)

同樣，也為輸出數據準備整數序列

1. unique_y = list(set(y))  2. y_note_to_int = dict((note_, number) for number, note_ in enumerate(unique_y))   3. y_seq=np.array([y_note_to_int[i] for i in y])

讓我們保留80％的數據用于訓練，其余20％的用于評估：

1. from sklearn.model_selection import train_test_split  2. x_tr, x_val, y_tr, y_val = train_test_split(x_seq,y_seq,test_size=0.2,random_state=0)

構建模型

我在這里定義了2種架構– WaveNet和LSTM。請嘗試兩種架構，以了解WaveNet架構的重要性。

1. def lstm():  2.   model = Sequential()  3.   model.add(LSTM(128,return_sequences=True))  4.   model.add(LSTM(128))  5.   model.add(Dense(256))  6.   model.add(Activation('relu'))  7.   model.add(Dense(n_vocab))  8.   model.add(Activation('softmax'))  9.   model.compile(loss='sparse_categorical_crossentropy', optimizer='adam')  10.   return model

我簡化了WaveNet的架構，沒有添加殘差連接和跳躍連接，因為這些層的作用是提高收斂速度(WaveNet以原始音頻波作為輸入)。但在我們的例子中，輸入是一組音符和和弦，因為我們在生成音樂:

1. from keras.layers import *  2. from keras.models import *  3. from keras.callbacks import *  4. import keras.backend as K  5.   6. K.clear_session()  7. model = Sequential()  8.       9. #embedding layer  10. model.add(Embedding(len(unique_x), 100, input_length=32,trainable=True))   11.   12. model.add(Conv1D(64,3, padding='causal',activation='relu'))  13. model.add(Dropout(0.2))  14. model.add(MaxPool1D(2))  15.       16. model.add(Conv1D(128,3,activation='relu',dilation_rate=2,padding='causal'))  17. model.add(Dropout(0.2))  18. model.add(MaxPool1D(2))  19.   20. model.add(Conv1D(256,3,activation='relu',dilation_rate=4,padding='causal'))  21. model.add(Dropout(0.2))  22. model.add(MaxPool1D(2))  23.             24. #model.add(Conv1D(256,5,activation='relu'))      25. model.add(GlobalMaxPool1D())  26.       27. model.add(Dense(256, activation='relu'))  28. model.add(Dense(len(unique_y), activation='softmax'))  29.       30. model.compile(loss='sparse_categorical_crossentropy', optimizer='adam')  31.   32. model.summary()

定義回調以在訓練期間保存最佳模型：

mc=ModelCheckpoint('best_model.h5', monitor='val_loss', mode='min', save_best_only=True,verbose=1)

讓我們使用128的批大小將模型訓練50個epoch:

history = model.fit(np.array(x_tr),np.array(y_tr),batch_size=128,epochs=50,validation_data=(np.array(x_val),np.array(y_val)),verbose=1, callbacks=[mc])

導入最好的模型：

1. #loading best model  2. from keras.models import load_model  3. model = load_model('best_model.h5')

是時候創作我們自己的音樂了。我們將按照推斷階段中提到的步驟進行預測。

1. import random  2. ind = np.random.randint(0,len(x_val)-1)  3.   4. random_music = x_val[ind]  5.   6. predictions=[]  7. for i in range(10):  8.   9.     random_music = random_music.reshape(1,no_of_timesteps)  10.   11.     prob  = model.predict(random_music)[0]  12.     y_pred= np.argmax(prob,axis=0)  13.     predictions.append(y_pred)  14.   15.     random_music = np.insert(random_music[0],len(random_music[0]),y_pred)  16.     random_music = random_music[1:]  17.       18. print(predictions)

現在，我們將整數還原為音符。

1. x_int_to_note = dict((number, note_) for number, note_ in enumerate(unique_x))   2. predicted_notes = [x_int_to_note[i] for i in predictions]

最后一步是將預測結果轉換回MIDI文件。讓我們定義一個函數來完成此任務。

1. def convert_to_midi(prediction_output):  2.      3.     offset = 0  4.     output_notes = []  5.   6.     # create note and chord objects based on the values generated by the model  7.     for pattern in prediction_output:  8.           9.         # pattern is a chord  10.         if ('.' in pattern) or pattern.isdigit():  11.             notes_in_chord = pattern.split('.')  12.             notes = []  13.             for current_note in notes_in_chord:  14.                   15.                 cn=int(current_note)  16.                 new_note = note.Note(cn)  17.                 new_note.storedInstrument = instrument.Piano()  18.                 notes.append(new_note)  19.                   20.             new_chord = chord.Chord(notes)  21.             new_chord.offset = offset  22.             output_notes.append(new_chord)  23.               24.         # pattern is a note  25.         else:  26.               27.             new_note = note.Note(pattern)  28.             new_note.offset = offset  29.             new_note.storedInstrument = instrument.Piano()  30.             output_notes.append(new_note)  31.   32.         # increase offset each iteration so that notes do not stack  33.         offset += 1  34.     midi_stream = stream.Stream(output_notes)  35.     midi_stream.write('midi', fp='music.mid')

將預測結果轉換為音樂文件：

convert_to_midi(predicted_notes)

奧利給，對嗎，但你的學習不該止步于此。請記住，我們已經構建了一個基準(baseline)模型。

有很多方法可以進一步提高模型的性能: