
機器學習和深度學習一直是業界的熱門話題。品牌領先于功能,導致深度學習在許多人工智能應用中被過度使用。
這篇文章將提供對約束求解的快速理解,這是一個強大但未被充分利用的方法,可以解決人工智能和其他計算機科學領域的大量問題,例如物流和調度時間推理和圖形問題。
解決現實問題
讓我們來考慮一個事實性的和高度話題性的問題。
病人人數正在上升。醫院必須迅速組織起來治療病人。
世界上需要一種算法,在疾病嚴重程度、患者年齡和位置、醫院容量和設備等多個標準下,將感染者和醫院匹配起來。

許多人會說,神經網絡將是最適合它的:它可以有不同的配置,廣泛的參數范圍,可以根據需要減少到一個獨特的解決方案。
然而,也有一些不利因素會破壞這個方案:
- 模型需要訓練,因此需要以前案例的歷史數據,
- 清理和整合數據集會浪費很多時間,
- 各種體系結構都需要通過冗長的訓練并且要進行測試。
另一方面,如果用一個布爾可滿足性問題來描述,在不確定多項式時間(NP完全問題)中仍然給出次優解,并且不需要任何歷史數據的情況下,不會有上述任何缺點。
這篇文章幫助你快速一覽CSPs。理論和問題的表述將被忽略。有關更嚴格的方法,請參考論文,論文在文章的末尾
抽象問題
這篇文章將介紹約束編程,旨在解決這個案例。上面那張圖說明了我們算法的輸出,應該該算法將感染者與醫院匹配。現有幾個框架用于約束求解。google Optimization Tools(又稱Tools)是一個用于解決組合優化問題的開源軟件套件。我們的問題將使用Python中的這個框架進行建模。
from ortools.sat.python import cp_model
colab:https://colab.research.google.com/drive/1vFkt5yIQtyelqvCh2TsJ9UDeM5miXqui
參數
現在,讓我們將問題簡化為4個參數(1):
- 感染者所在地
- 感染者的嚴重程度
- 醫院位置
- 每家醫院的床位數
讓我們用python定義這些參數:
# 醫院數量
n_hospitals = 3
# 感染者人數
n_patients = 200
# 每家醫院的床位數
n_beds_in_hospitals = [30,50,20]
# 病人位置,tuple (x,y)
patients_loc = [(randint(0, 100), randint(0, 100)) for _ in range(n_patients)]
# 醫院位置,tuple (x,y)
hospitals_loc = [(randint(0, 100), randint(0, 100)) for _ in range(n_hospitals)]
# 病人嚴重等級 1~5
patients_severity = [randint(1, 5) for _ in range(n_patients)]
變量
約束滿足問題由一組變量組成,這些變量必須以滿足一組約束。
- 令I為醫院的集合
- 令$J_i$為醫院i的床位集合
- 令$K$為病人集合
定義變量的索引族:
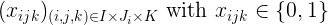
如果在醫院i中,床j由病人k取走,則$x_{ijk} = 1$。為了將醫院的每一張床與一個病人聯系起來,我們的目標是找到一組滿足所有約束條件的變量。
我們可以將這些變量添加到模型中:
model = cp_model.CpModel()
x = {}
for i in range(n_hospitals):
for j in range(n_beds_in_hospitals[i]):
for k in range(n_patients):
x[(i,j,k)] = model.NewBoolVar("x(%d,%d,%d)" % (i,j,k))
硬約束
硬約束定義了模型的目標。它們是必不可少的,如果它們得不到解決,就無法解決問題:
- 每張床上最多只能有一個人
- 每個人最多只能有一張床
讓我們關注第一個硬約束。對于每家醫院的每一張床,我:
- 要么有一個唯一的病人k,
- 要么床是空的。
因此,可以用以下方式表示:
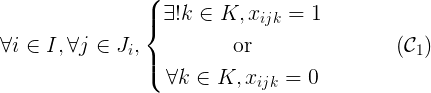
我們的求解器是一個組合優化求解器,它只能處理整數約束。因此,必須轉化為一個整數方程:
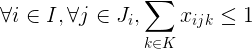
這個不等式可以加到我們的模型中。
# 每張床最多只能住一個人
for i in range(n_hospitals):
for j in range(n_beds_in_hospitals[i]):
model.Add(sum(x[(i,j,k)] for k in range(n_patients)) <= 1)
接下來,第二個硬約束:對于每個患者k:
- 要么他在一個唯一的病床上j在一個唯一的醫院i
- 要么他在家。

同理,可以轉化為一個整數不等式:

最后,可以將此約束添加到模型中。
# 每個人最多只能睡一張床
for k in range(n_patients):
inner_sum = []
for i in range(n_hospitals):
inner_sum.Append(sum(x[(i,j,k)] for j in range(n_beds_in_hospitals[i])))
model.Add(sum(inner_sum) <= 1)
軟約束
接下來是軟約束。這些都是非常需要的:我們的解決方案必須盡可能滿足它們,但它們不是找到解決方案的必要條件:
- 每個病人都應該躺在床上
- 每個人都應該由最近的醫院處理
- 病床不足時,應先處理病情嚴重的病人
當硬約束被建模為等式或不等式時,軟約束是最小化或最大化的表達式。
設Ω為滿足硬約束的所有解的集合。
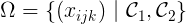
每一個病人都應該被安排在一張床上,這意味著最大限度地增加被占用的床的數量。
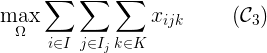
每個人都應該由最近的醫院處理,以盡量減少每個病人與其指定醫院之間的距離。
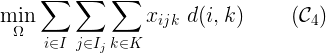
如果沒有足夠的床位,應首先處理病情嚴重的病人,以最大限度地提高所有處理病人的總嚴重程度。通過表示sev(k)患者k的嚴重程度:
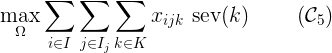
然后我們可以將所有軟約束簡化為一個目標:

需要注意的是:這些軟約束沒有相同的定義域。
- 患者最大化約束范圍從0到n,其中n是患者數,
- 病情嚴重性限制范圍從0到5n
- 距離約束范圍從0到所有i和k的最大歐幾里得距離。
考慮到所有這些約束具有相同的優先級,我們必須定義懲罰因子來平衡不同的約束。
下面是相應的代碼:
# 整數的距離函數
idist = lambda xy1, xy2: int(((xy1[0]-xy2[0])**2 + (xy1[1]-xy2[1])**2)**0.5)
gain_max_patients = 140
gain_severity = int(140/5)
gain_distance = -1
#最大化的目標
soft_csts = []
for i in range(n_hospitals):
for j in range(n_beds_in_hospitals[i]):
for k in range(n_patients):
factor =
gain_max_patients
+ gain_distance * idist(hospitals_loc[i], patients_loc[k])
+ gain_severity * patients_severity[k]
soft_csts.append(factor * x[(i,j,k)])
model.Maximize(sum(soft_csts))
求解
現在我們可以啟動求解器了。它將試圖在指定的時間限制內找到最優解。如果無法找到最優解,則返回最近的次優解。
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = 60.0
status = solver.Solve(model)
在我們的例子中,求解器在2.5秒內返回一個最優解。
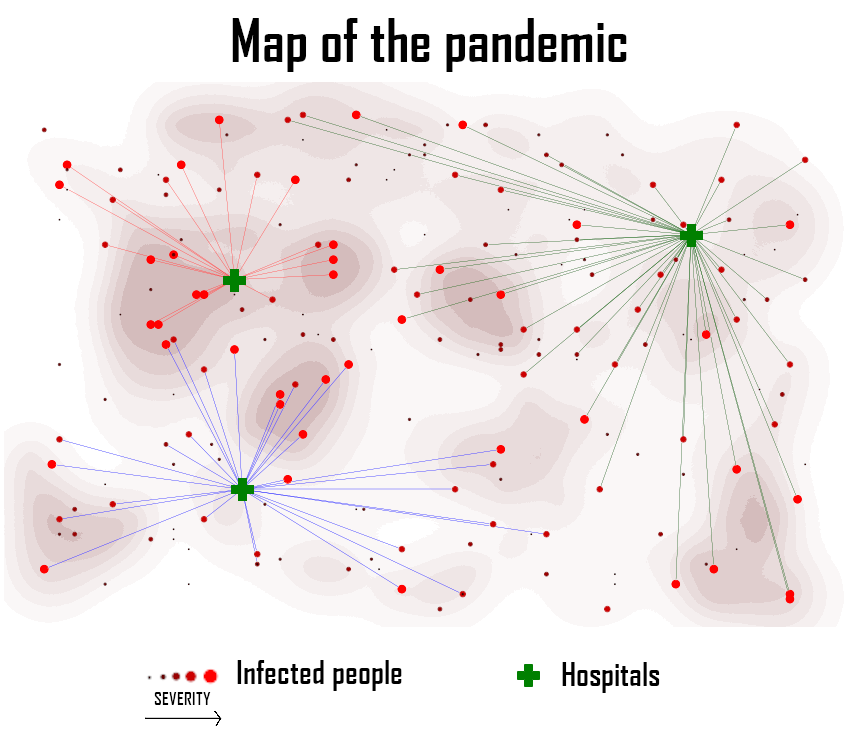
結論
要創建這個解決方案,只需要1小時的研究和30分鐘的編程。
如果使用深度學習,要進行幾天的數據清理,至少一天測試不同的架構,另一天進行訓練。
此外,如果模型良好,CP-SAT模型是非常健壯的。下面是不同模擬參數的結果。結果在許多不同的情況下仍然是一致的,隨著模擬參數的增加(3000名患者,1000張病床),解決方案推斷只需不到3分鐘。

當然,csp幾乎不適用于計算機視覺和NLP等主題,在這些主題中,深度學習有時是最好的方法。然而,在物流、調度和計劃方面,這往往是可以實現的方法。
深度學習的炒作激發了一些人嘗試一些瘋狂的舉動來獲得認可。有時,最好還是通過閱讀幾篇關于你正在研究的問題的調查報告再想想你應該如何解決。
引用
[1] Jingchao Chen, Solving Rubik’s Cube Using SAT Solvers, arXiv:1105.1436, 2011.
[2] Biere, A., Heule, M., and van Maaren, H. Handbook of satisfiability, volume 185. IOS press, 2009a
[3] Knuth, D. E., The art of computer programming, Volume 4, Fascicle 6: Satisfiability. Addison-Wesley Professional, 2015
[4] Vipin Kumar, Algorithms for constraint-satisfaction problems: a survey, AI Magazine Volume 13, Issue 1, 1992.






