在這一節，我們將簡要介紹不同類型的機器學習，并重點關注它們的主要特點和差異。在接下來的部分中，我們將討論非正式定義，以及正式定義。如果你不熟悉討論中涉及的數學概念，則可以跳過詳細信息。但是，研究所有未知的理論因素是非常明智的，因為它們對于理解后面章節的概念至關重要。

1.3.1　有監督學習算法

在有監督的場景中，模型的任務是查找樣本的正確標簽，假設在訓練集時標記正確，并有可能將估計值與正確值進行比較。有監督這個術語源自外部教學代理的想法，其在每次預測之后提供精確和即時的反饋。模型可以使用此類反饋作為誤差的度量，從而減少錯誤所需的更正。

更正式地說，如果我們假設一個數據生成過程，數據集

的獲取如下：

其中

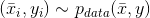
且

如1.2節所述，所有樣本必須是從數據生成過程中統一采樣的獨立且同分布（Independent and Identically Distributed，IID）的值。特別地，所有類別必須代表實際分布（例如，如果p( y = 0) = 0.4且p( y = 1) = 0.6，則該比例應為40%或60%）。但是，為了避免偏差，當類之間的差異不是很大時，合理的選擇是完全統一的采樣，并且對于y = 1,2,…,M是具有相同數量的代表。

通用分類器

可以通過兩種方式建模。

輸出預測類的參數化函數。
參數化概率分布，輸出每個輸入樣本的類概率。

對于第一種情況，我們有：

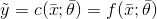
且

是一個錯誤的測量結果

考慮整個數據集X，可以計算全局成本函數L：

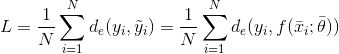
由于L僅取決于參數向量（xi和yi是常數），因此通用算法必須找到最小化成本函數的最佳參數向量。例如在回歸問題（標簽是連續的）中，誤差度量可以是實際值和預測值之間的平方誤差：

這種成本函數可以用不同的方式優化（特定算法特有的），但一個非常常見的策略（尤其在深度學習中）是采用隨機梯度下降（Stochastic Gradient Descent，SGD）算法。它由以下兩個步驟的迭代組成。

使用少量樣本xi∈X計算梯度∇L（相對于參數向量）。
更新權重并在梯度的相反方向上移動參數（記住漸變始終指向最大值）。

對于第二種情況，當分類器是基于概率分布時，它應該表示為參數化的條件概率分布：

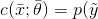
換句話說，分類器現在將輸出給定輸入向量y的概率。現在的目標是找到最佳參數集，它將獲得：

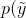
在前面的公式中，我們將pdata表示為條件分布。我們可以使用概率距離度量來進行優化，例如Kullback-Leibler散度DKL（DKL始終為非負，且僅當兩個分布相同時，DKL=0）：

通過一些簡單的操作，我們得到：

因此，生成的成本函數對應于p和pdata之間交叉熵的差值達到定值（數據生成過程的熵）。訓練策略現在是基于使用獨熱編碼表示的標簽（例如如果有兩個標簽0→（0,1）和1→（1,0），那么所有元素的總和必須始終等于1）并使用內在概率（例如在邏輯回歸中）或softmax濾波器（其將M值轉換為概率分布）輸出。

在這兩種情況下，很明顯隱藏教師模型的存在提供了一致的誤差測量，它允許模型相應地校正參數。特別地，第二種方法對達到我們的目的非常有用，因此如果你還不太清楚，我建議你進一步研究它（主要定義也可以在machine Learning Algorithms, Second Edition一書中找到）。

我們現在討論一個非常基本的監督學習示例，它是一個線性回歸模型，可用于預測簡單時間序列的演變。

有監督的hello world！

在此示例中，我們要展示如何使用二維數據執行簡單的線性回歸。特別地，假設我們有一個包含100個樣本的自定義數據集，如下所示：

import numpy as np
import pandas as pd
T = np.expand_dims(np.linspace(0.0, 10.0, num=100), axis=1)
X = (T * np.random.uniform(1.0, 1.5, size=(100, 1))) + 
np.random.normal(0.0, 3.5, size=(100, 1))
df = pd.DataFrame(np.concatenate([T, X], axis=1), columns=['t', 'x'])

　

我們還創建了一個pandas的DataFrame，因為使用seaborn庫創建繪圖更容易。在本書中，通常省略了圖表的代碼（使用Matplotlib或seaborn），但它始終存在于庫中。

我們希望用一種綜合的方式表示數據集，如下所示：

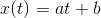
此任務可以使用線性回歸算法執行，如下所示：

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(T, X)
print('x(t) = {0:.3f}t + {1:.3f}'.format(lr.coef_[0][0], lr.intercept_[0]))

最后一個命令的輸出如下：

X(t) = 1.169t + 0.628

我們還可以將數據集與回歸線一起繪制，獲得視覺確認，如圖1-4所示。

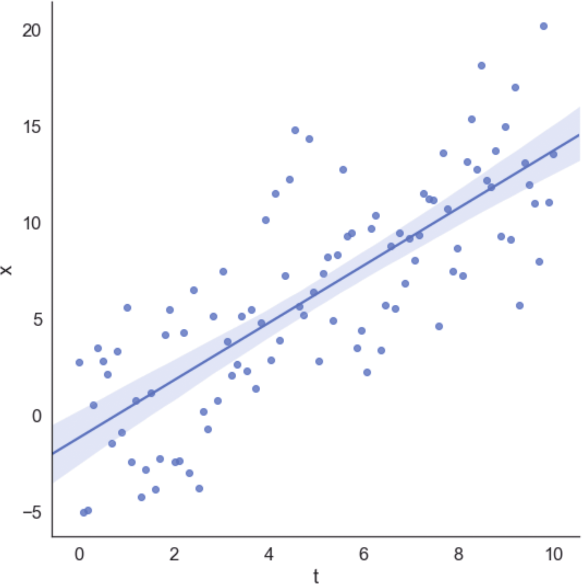
圖1-4　數據集與回歸線

在該示例中，回歸算法最小化了平方誤差成本函數，試圖減小預測值與實際值之間的差異。由于對稱分布，所以高斯（空均值）噪聲對斜率的影響最小。

1.3.2　無監督學習算法

很容易想象在無監督的場景中，沒有隱藏的老師，因此主要目標與最小化基本事實的預測誤差無關。實際上，在這種背景下，相同的基本事實的概念具有略微不同的含義。事實上，在使用分類器時，我們希望訓練樣本出現一個零錯誤（這意味著除了真正類之外的其他類永遠不會被接受為正確類）。

相反，在無監督問題中，我們希望模型在沒有任何正式指示的情況下學習一些信息。這種情況意味著唯一可以學習的因素是樣本本身包含的。因此，無監督算法通常旨在發現樣本之間的相似性和模式，或者在給定一組從中得出的向量的情況下，再現輸入分布。現在讓我們分析一些最常見的無監督模型類別。

1．聚類分析

聚類分析（通常稱為聚類）是我們想要找出大量樣本中共同特征的示例。在這種情況下，我們總是假設存在數據生成過程

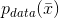
，并且將數據集X定義為：

其中

且

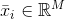
聚類算法基于一個隱含假設，即樣本可以根據其相似性進行分組。特別是當給定兩個向量，相似性函數被定義為度量函數的倒數或相反數。例如，如果我們在歐幾里得空間中，則有：

且

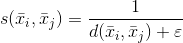
在前面的公式中，引入了常數ε以避免除以零。很明顯，d(a,c) < d(a,b) ⇒ s(a,c) > s(a,b)。因此，給定每個聚類

的代表，我們可以根據規則創建一組分配的向量：

換句話說，聚類包含代表距離同所有其他代表相比最小的所有元素。這意味著聚類包含同所有代表相比與代表的相似性最大的樣本。此外，在分配之后，樣本獲得與同一聚類的其他成員共享其功能的權利。

事實上，聚類分析最重要的應用之一是嘗試提高被認為相似樣本的同質性。例如推薦引擎可以基于用戶向量的聚類（包含有關用戶興趣和購買產品的信息）來進行推薦。一旦定義了組，屬于同一聚類的所有因素都被認為是相似的，因此我們被隱式授權共享差異。如果用戶A購買了產品P并對其進行了積極評價，我們可以向沒有購買產品的用戶B推薦此商品，反之亦然。該過程看似隨意，但是當因素的數量很大并且特征向量包含許多判別因素（例如評級）時，因素就變得非常有效了。

2．生成模型

另一種無監督方法是基于生成模型。這個概念與我們已經討論的有監督算法的概念沒有太大區別，但在這種情況下，數據生成過程不包含任何標簽。因此，我們的目標是對參數化分布進行建模并優化參數，以便將候選分布與數據生成過程之間的距離最小化：

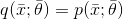
該過程通常基于Kullback-Leibler散度或其他類似度量：

在訓練階段結束時，我們假設L→0，所以p≈pdata。通過這種方式，我們不會將分析限制在可能樣本的子集，而是限制在整個分布。使用生成模型，我們可以繪制與訓練過程選擇樣本截然不同的新樣本，但它們始終屬于相同的分布。因此，它們（可能）總是可以接受的。

例如生成式對抗網絡（Generative Adversarial Network，GAN）是一種特殊的深度學習模型，它能夠學習圖像集的分布，生成與訓練樣本幾乎無法區分的新樣本（從視覺語義的角度來看）。無監督學習是本書的主題，因此我們不會在此處進一步討論GAN。所有這些概念將在第9章（用實際例子）進行深入討論。

3．關聯規則

我們正在考慮的最后一種無監督方法是基于關聯規則的，它在數據挖掘領域非常重要。常見的情形是由一部分商品組成的商業交易集合，目標是找出商品之間最重要的關聯（例如購買Pi和Pj的概率為70%）。特定算法可以有效地挖掘整個數據庫，突出所有可以考慮到的戰略和物流目的之間的關系。例如在線商店可以使用這種方法來促銷那些經常與其他商品一起購買的商品。此外，預測方法允許通過建議所有很可能售罄的商品來簡化供應流程，這要歸功于其他項目的銷售增加。

在這一點上，讀者了解無監督學習的實際例子是有幫助的。不需要特別的先決條件，但你最好具備概率論的基本知識。

4．無監督的hello world！

由于本書完全致力于無監督算法的講解，在此不將簡單的聚類分析顯示為hello world！示例，而是假設一個非常基本的生成模型。假設我們正在監控每小時到車站的列車數量，因為我們需要確定車站所需的管理員數量。特別地，要求每列列車至少有1名管理員，每當管理員數量不足時，我們將被罰款。

此外，在每小時開始時發送一個組更容易，而不是逐個控制管理員。由于問題非常簡單，我們也知道泊松分布是一個好的分布，參數μ同樣也是平均值。從理論上講，我們知道這種分布可以在獨立的主要假設下有效地模擬在固定時間范圍內發生的事件的隨機數。在一般情況下生成模型基于參數化分布（例如神經網絡），并且不對其系列進行具體假設。僅在某些特定情況下（例如高斯混合），選擇具有特定屬性的分布是合理的，并且在不損失嚴謹性的情況下，我們可以將該示例視為此類方案之一。

泊松分布的概率質量函數為：

此分布描述了在預定義的間隔內觀察k個事件的概率。在我們的例子中，間隔始終是1小時，我們希望觀測10多趟列車，然后估計概率。我們如何才能獲得μ的正確數值？

最常見的策略稱為最大似然估計（Maximum Likelihood Estimation，MLE）。該策略通過收集一組觀測值，然后找到μ的值，該值使分布生成所有點的概率最大化。

假設我們已經收集了 N 個觀測值（每個觀測值是一小時內到達的列車數量），則相對于所有樣本的μ的似然度是在使用以下公式計算的概率分布下所有樣本的聯合概率μ（為簡單起見，假設為IID）：

當我們使用乘積和指數時，計算對數似然是一種常見的規則：

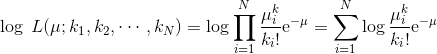
一旦計算出對數似然，我們就可以將μ的導數設置為0，以便找到最佳值。在這種情況下，我們省略了證明（直接獲得）并直接得出μ的最大似然估計值：

很幸運的是最大似然估計值只是到達時間的平均值。這意味著，如果我們觀察到N個平均值為μ的值，則有很大可能生成它們的泊松分布，其特征系數為μ。因此，從這種分布中抽取的任何其他樣本將與觀察到的數據集兼容。

我們現在可以從第一次模擬開始。假設我們在工作日的下午收集了25個觀察結果，如下所示：

import numpy as np
obs = np.array([7, 11, 9, 9, 8, 11, 9, 9, 8, 7, 11, 8, 9, 9, 11, 7, 10, 9, 10, 9, 7, 8, 9, 10, 13])
mu = np.mean(obs)
print('mu = {}'.format(mu))

最后一個命令的輸出如下：

mu = 9.12

因此，每小時平均到達9趟列車。初始分布的直方圖如圖1-5所示。

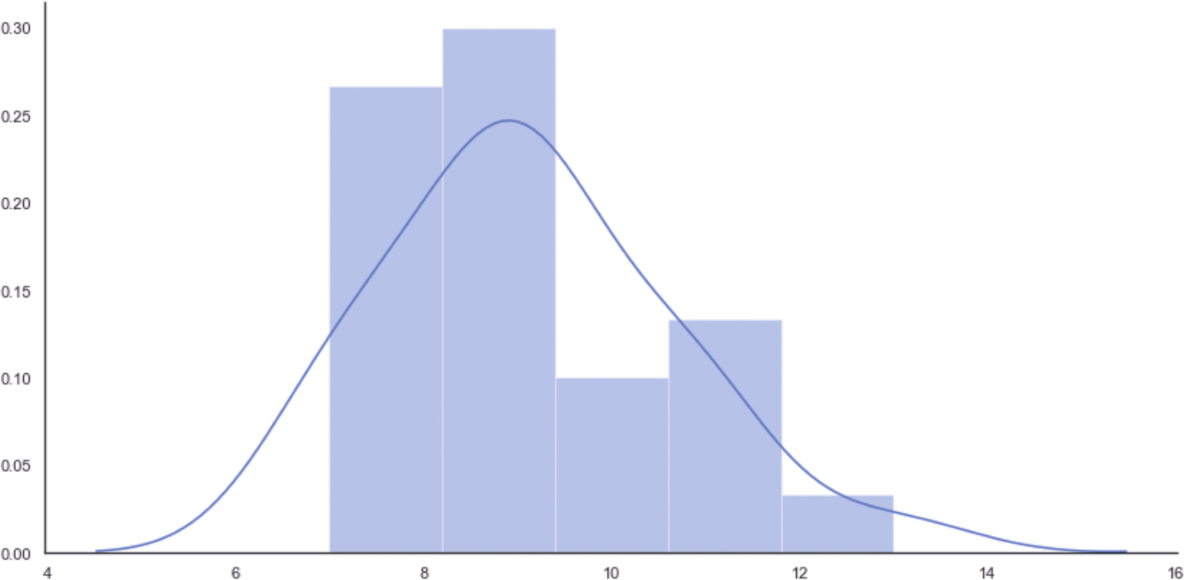
圖1-5　初始分布的直方圖

要計算請求的概率，我們需要使用累積分布函數（Cumulative Distribution Function，CDF），它在SciPy中實現（在scipy.stats包中）。特別地，由于我們感興趣的是觀察到的列車數量超過固定值的概率，因此有必要使用與1-CDF相對應的生存函數（Survival Function，SF），如下所示：

from scipy.stats import poisson
print('P(more than 8 trains) = {}'.format(poisson.sf(8, mu)))
print('P(more than 9 trains) = {}'.format(poisson.sf(9, mu)))
print('P(more than 10 trains) = {}'.format(poisson.sf(10, mu)))
print('P(more than 11 trains) = {}'.format(poisson.sf(11, mu)))

上述代碼段的輸出如下所示：

P(more than 8 trains) = 0.5600494497386543
P(more than 9 trains) = 0.42839824517059516
P(more than 10 trains) = 0.30833234660452563
P(more than 11 trains) = 0.20878680161156604

正如預期的那樣，能觀測10多趟列車的概率很低（30%），派10名管理員似乎不合理。但是，由于我們的模型是自適應的，我們可以繼續收集觀測值（例如在清晨），如下所示：

new_obs = np.array([13, 14, 11, 10, 11, 13, 13, 9, 11, 14, 12, 11, 12,14,
8, 13, 10, 14, 12, 13, 10, 9, 14, 13, 11, 14, 13, 14])
obs = np.concatenate([obs, new_obs])
mu = np.mean(obs)
print('mu = {}'.format(mu))

μ的新值如下所示：

mu = 10.641509433962264

現在平均每小時 11 趟列車。假設我們收集了足夠的樣本（考慮所有潛在的事故），我們可以重新估計概率，如下所示：

print(P(more than 8 trains) = {}'.format(poisson.sf(8, mu)))
print(P(more than 9 trains) = {}'.format(poisson.sf(9, mu)))
print(P(more than 10 trains) = {}'.format(poisson.sf(10, mu)))
print(P(more than 11 trains) = {}'.format(poisson.sf(11, mu)))

輸出如下：

P(more than 8 trains) = 0.734624391080037
P(more than 9 trains) = 0.6193541369812121
P(more than 10 trains) = 0.49668918740243756
P(more than 11 trains) = 0.3780218948425254

使用新數據集觀測超過9趟列車的概率約為62%（這證實了我們最初的選擇），但現在觀測超過10趟列車的概率約為50%。由于我們不想承擔支付罰款的風險（這比管理員的成本高），因此最好派10名管理員。為了得到進一步的確認，我們決定從分布中抽取2000個值，如下所示：

syn = poisson.rvs(mu, size=2000)

相應的直方圖如圖1-6所示。

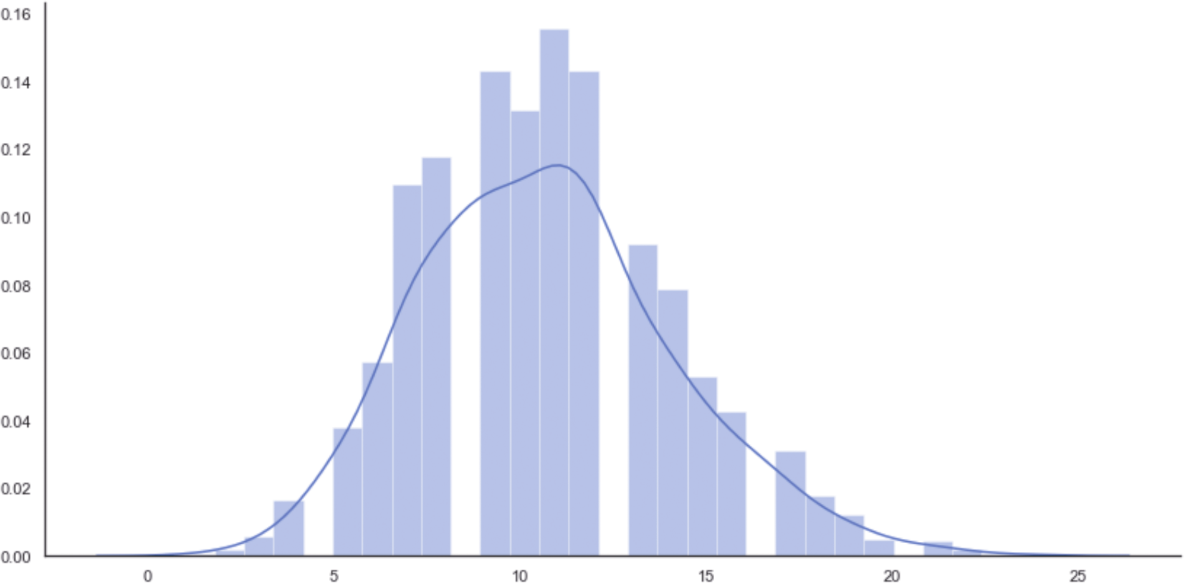
圖1-6　從最終泊松分布中抽取2000個值的直方圖

該圖在10（表示10名管理員）之后（非常接近11時）達到峰值，然后從k=13開始快速衰減，這是使用有限數據集發現的（比較直方圖的形狀以進一步確認）。但是，在這種情況下，我們正在生成無法存在于觀察集中的潛在樣本。MLE保證了概率分布與數據一致，并且新樣本將相應地進行加權。這個例子非常簡單，其目的只是展示生成模型的動態性。

我們將在本書的后續章節中討論許多更復雜的模型和示例。許多算法常見的一個重要技術在于不是選擇預定義的分布（這意味著先驗知識），而是選擇靈活的參數模型（例如神經網絡）來找出最優分布。只有基礎隨機過程存在較高的置信度時，優先選擇預定義（如本例所示）才合理。在其他情況下，最好避免任何假設，只依賴數據，以便找到數據生成過程中的最適當的近似值。

1.3.3　半監督學習算法

半監督場景可以被視為標準監督場景，它利用了一些屬于無監督學習技術的特征。事實上，當很容易獲得大的未標記數據集，而標簽成本又非常高時，就會出現一個非常普遍的問題。因此，只標記部分樣本并將標簽傳播到所有未標記樣本，這些樣本與標記樣本的距離就會低于預定義閾值。如果從單個數據生成過程中抽取數據集并且標記的樣本均勻分布，則半監督算法可以實現與有監督算法相當的精度。在本書中，我們不討論這些算法，但有必要簡要介紹兩個非常重要的模型。

標簽傳播。
半監督支持向量機。

第一個稱為標簽傳播（Label Propagation），其目的是將一些樣本的標簽傳播到較大的群體。我們可以通過圖形來實現該目標，其中每個頂點表示樣本并且每條邊都使用距離函數進行加權。通過迭代，所有標記的樣本將其標簽值的一小部分發送給它們所有的近鄰，并且重復該過程直到標簽停止變化。該系統具有最終穩定點（即無法再演變的配置），算法可以通過有限的迭代次數輕松到達該點。

標簽傳播在某些樣本可以根據相似性度量進行標記的情況下非常有用。例如在線商店可能擁有大量客戶，但只有10%的人透露了自己的性別。如果特征向量足夠豐富以表示男性和女性用戶的常見行為，則可以使用標簽傳播算法來猜測未公開信息的客戶性別。當然，請務必記住，所有分配都基于相似樣本具有相同標簽的假設。在許多情況下都是如此，但是當特征向量的復雜性增加時，也可能會產生誤導。

第二個重要的半監督算法系列是基于標準支持向量機（Support Vector Machine，SVM）的，對包含未標記樣本的數據集的擴展。在這種情況下，我們不想傳播現有標簽，而是傳播分類標準。換句話說，我們希望使用標記數據集來訓練分類器，并將分類規則擴展到未標記的樣本。

與僅能評估未標記樣本的標準過程相反，半監督SVM使用它們來校正分離超平面。假設始終基于相似性：如果A的標簽為1，而未標記樣本B的d（A，B）<ε（其中ε是預定義的閾值），則可以合理地假設B的標簽也是1。通過這種方式，即使僅手動標記了一個子集，分類器也可以在整個數據集上實現高精度。與標簽傳播類似，這種類型的模型只有在數據集的結構不是非常復雜時，特別是當相似性假設成立時（不幸的是，在某些情況下，找到合適的距離度量非常困難，因此許多類似的樣本確實不相似，反之亦然）才是可靠的。

1.3.4　強化學習算法

強化學習可以被視為有監督的學習場景，其中隱藏教師僅在模型的每個決策后提供近似反饋。更正式地說，強化學習的特點是代理和環境之間的持續互動。前者負責決策（行動），最終增加其回報，而后者則為每項行動提供反饋。反饋通常被視為獎勵，其價值可以是積極的（行動已成功）或消極的（行動不能復用）。當代理分析環境（狀態）的不同配置時，每個獎勵必須被視為綁定到元組（行動，狀態）。因此，我們的最終目標是找到一種方針（建議在每種狀況下采取最佳行動的一種策略），使預期總回報最大化。

強化學習的一個非常經典的例子是學習如何玩游戲的代理。在一個事件中，代理會測試所有遇到狀態中的操作并收集獎勵。算法校正策略以減少非積極行為（即獎勵為正的行為）的可能性，并增加在事件結束時可獲得的預期總獎勵。

強化學習有許多有趣的應用，這些應用并不僅限于游戲。例如推薦系統可以根據用戶提供的二進制反饋（例如拇指向上或向下）來更正建議。強化學習和有監督學習之間的主要區別在于環境提供的信息。事實上，在有監督的場景中，更正通常與其成比例，而在強化學習中，必須分析一系列行動和未來的獎勵。因此，更正通常基于預期獎勵的估計，并且它們的影響受后續行動的價值影響。例如有監督模型沒有內存，因此其更正是立竿見影的，而強化學習代理必須考慮一個事件的部分展開，以決定一個操作是否是負的。

強化學習是機器學習的一個有趣分支。遺憾的是，這個主題超出了本書的范圍，因此我們不會詳細討論它（你可以在Hands-On Reinforcement Learning with Python和Mastering Machine Learning Algorithms中找到更多細節）。

本文摘自：《Python無監督學習》